题目内容
7. 如图,正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,平面AMN与平面EFBD间的距离为$\frac{8}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,平面AMN与平面EFBD间的距离为$\frac{8}{3}$.
分析 连结A1C1交MN于P点,交EF于点Q,连结AC交BD于点O,分别连结PA、QO.由已知得四边形PAOQ为平行四边形,由此能证明平面AMN∥平面EFBD.
解答 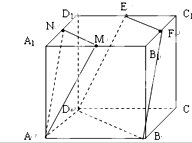 解:连结A1C1交MN于P点,交EF于点Q,
解:连结A1C1交MN于P点,交EF于点Q,
连结AC交BD于点O,分别连结PA、QO.
∵M、N为A1B1、A1D1的中点,
∴MN∥EF.而EF?面EFBD.
∴MN∥面EFBD.∵PQ∥AO,PQ=AO
∴四边形PAOQ为平行四边形.∴PA∥QO.
而QO?平面EFBD,∴PA∥平面EFBD,
且PA∩MN=P,PA、MN?面AMN.
∴平面AMN∥平面EFBD,
∴平面AMN与平面EFBD间的距离即E到平面AMN的距离,
设E到平面AMN的距离为h,
有VA-MNE=VE-AMN,S△MNE=$\frac{1}{2}$×2×4=4,
AM=AN=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,MN=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,根据勾股定理得AG=3$\sqrt{2}$,S△AMN=$\frac{1}{2}$×3$\sqrt{2}$×2$\sqrt{2}$=6,
VA-MNE=$\frac{1}{3}$×4×4=$\frac{16}{3}$.
∴h=$\frac{3{V}_{A-MNE}}{{S}_{△AMN}}$=$\frac{16}{6}$=$\frac{8}{3}$.
点评 本题考查了空间直线的位置关系,平行垂直问题,难度适中,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.若BC边上存在两个点Q使得PQ⊥DQ.则a的取值范围是( )
| A. | (1,+∞) | B. | [1,2) | C. | (2,+∞) | D. | [2,4] |
16.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则$\frac{a}{b}$的值( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
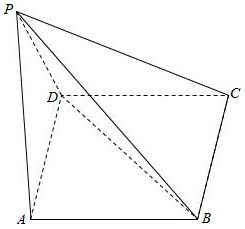 如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.
如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.