题目内容
对任意复数z=a+bi(a,b ∈R),i为虚数单位,则下列结论中正确的是( )
A.z- =2a =2a |
B.z· =|z|2 =|z|2 |
C. =1 =1 |
D. ≥0 ≥0 |
B
解析试题分析:因为z=a+bi,所以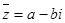 ,所以
,所以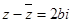 ,故A错,又
,故A错,又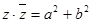 ,而
,而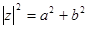 ,故z·
,故z· =|z|2,选B.
=|z|2,选B.
考点:1.复数的概念; 2.复数的运算.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知复数 在复平面内对应的点分别为
在复平面内对应的点分别为 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
若复数z满足iz=2+4i,则在复平面内z对应的点的坐标是 ( )
| A.(2,4) | B.(2,-4) | C.(4,-2) | D.(4,2) |
设复数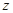 满足
满足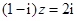 ,则
,则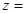 ( )
( )
A.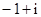 | B.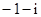 | C.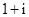 | D.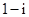 |
复数z满足 ,则复数z=( )
,则复数z=( )
A.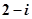 | B.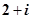 | C.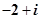 | D.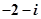 |
已知复数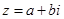
 ,且
,且 为实数,则
为实数,则 ( )
( )
A. | B. | C. | D. |
已知复数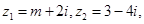 若
若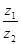 为实数,则实数
为实数,则实数 的值为( )
的值为( )
A.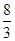 | B.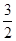 | C.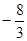 | D.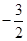 |
复数z=1-i,则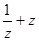 对应的点所在的象限为( )
对应的点所在的象限为( )
| A.第一象限 | B.第二象限 | C.第三象跟 | D.第四象限 |
复数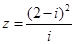
 为虚数单位,则
为虚数单位,则 ( )
( )
| A.25 | B. | C.6 | D. |