题目内容
己知平面内向量 =(3,3),
=(3,3), =(-1,2),
=(-1,2), =(4,1).
=(4,1).
(1)求实数t,使得2 +t
+t 与
与 共线;
共线;
(2)求实数k,使得 -k
-k 与
与 垂直.
垂直.
解:(1)由题意可得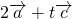 =(6+4t,6+t),
=(6+4t,6+t),
由向量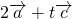 与
与 共线可得:
共线可得:
2(6+4t)-(-1)(6+t)=0,
解得t=-2;
(2)同理可得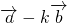 =(3+k,3-2k ),
=(3+k,3-2k ),
由向量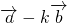 与
与 垂直可得:
垂直可得:
4(3+k)+(3-2k)=0,
解得k=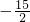
分析:(1)由向量的基本运算可得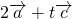 的坐标,由向量共线的充要条件可得t的值;(2)同理可得向量
的坐标,由向量共线的充要条件可得t的值;(2)同理可得向量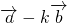 的坐标,由向量垂直的充要条件可得k的值.
的坐标,由向量垂直的充要条件可得k的值.
点评:本题考查向量的坐标运算和平行,垂直的充要条件,属基础题.
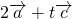 =(6+4t,6+t),
=(6+4t,6+t),由向量
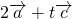 与
与 共线可得:
共线可得:2(6+4t)-(-1)(6+t)=0,
解得t=-2;
(2)同理可得
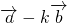 =(3+k,3-2k ),
=(3+k,3-2k ),由向量
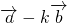 与
与 垂直可得:
垂直可得:4(3+k)+(3-2k)=0,
解得k=
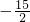
分析:(1)由向量的基本运算可得
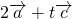 的坐标,由向量共线的充要条件可得t的值;(2)同理可得向量
的坐标,由向量共线的充要条件可得t的值;(2)同理可得向量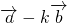 的坐标,由向量垂直的充要条件可得k的值.
的坐标,由向量垂直的充要条件可得k的值.点评:本题考查向量的坐标运算和平行,垂直的充要条件,属基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目