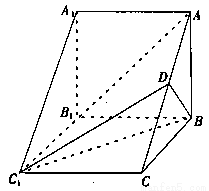
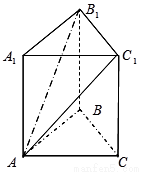
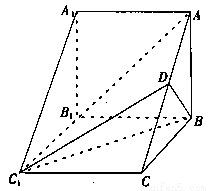
题目内容
如图,在三棱柱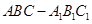 中,侧棱
中,侧棱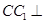 底面
底面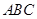 ,
,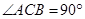 ,
,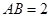 ,
,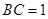 ,
,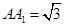 .
.

(1)证明: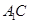
 平面
平面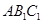 ;
;
(2)若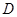 是棱
是棱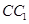 的中点,在棱
的中点,在棱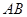 上是否存在一点
上是否存在一点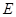 ,使
,使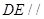 平面
平面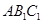 ?证明你的结论.
?证明你的结论.
【答案】
(1)见解析.(2)当点 为棱
为棱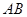 的中点时,
的中点时,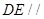 平面
平面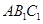 .证明见解析.
.证明见解析.
【解析】
试题分析:(1)要证明线面垂直,须证明直线与平面内的两条相交直线都垂直,一般要遵循“先找再作”的原则,对图形进行细致分析是关键.注意到 ,得到
,得到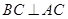 .
.
由侧棱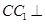 底面
底面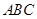 ,得到
,得到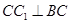 .从而得到
.从而得到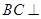 平面
平面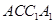 .
.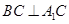 ,
,
利用 ,得到
,得到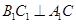 .结合四边形
.结合四边形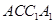 为正方形.
为正方形.
得到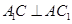 .推出
.推出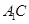
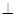 平面
平面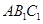 .
.
(2)对于这类存在性问题,往往是先通过对图形的分析,找“特殊点”,肯定其存在性,再加以证明.
注意到当点 为棱
为棱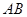 的中点时,取
的中点时,取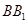 的中点
的中点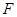 ,连
,连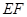 、
、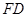 、
、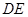 ,利用三角形相似,得到
,利用三角形相似,得到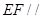 平面
平面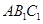 及
及 平面
平面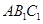 ,利用平面
,利用平面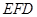
 平面
平面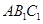 .推出
.推出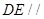 平面
平面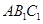 .
.
试题解析:(1)∵ ,∴
,∴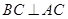 .
.
∵侧棱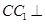 底面
底面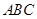 ,∴
,∴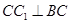 .
.
∵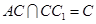 ,∴
,∴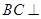 平面
平面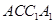 .
.
∵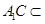 平面
平面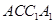 ,∴
,∴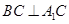 ,
,
∵ ,则
,则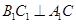 .
4分
.
4分
在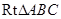 中,
中,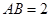 ,
,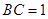 ,∴
,∴ .
.
∵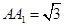 ,∴四边形
,∴四边形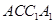 为正方形.
为正方形.
∴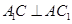 .
6分
.
6分
∵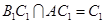 ,∴
,∴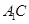
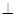 平面
平面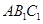 .
7分
.
7分
(2)当点 为棱
为棱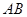 的中点时,
的中点时,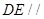 平面
平面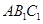 .
9分
.
9分
证明如下:
如图,取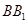 的中点
的中点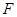 ,连
,连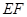 、
、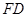 、
、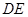 ,
,
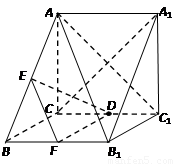
∵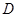 、
、 、
、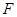 分别为
分别为 、
、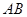 、
、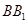 的中点,
的中点,
∴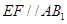 .
.
∵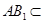 平面
平面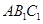 ,
,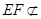 平面
平面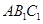 ,
,
∴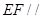 平面
平面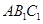 . 11分
. 11分
同理可证 平面
平面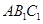 .
12分
.
12分
∵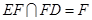 ,
,
∴平面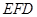
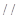 平面
平面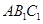 .
13分
.
13分
∵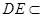 平面
平面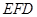 ,
,
∴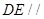 平面
平面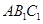 .
14分
.
14分
考点:立体几何的平行关系与垂直关系

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
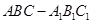 中,侧棱
中,侧棱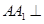 底面
底面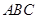 ,
,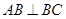 ,
,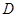 为
为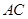 的中点,
的中点,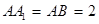 .
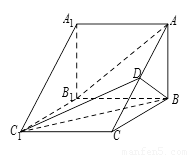
.
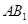 //平面
//平面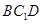 ;
;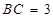 ,求四棱锥
,求四棱锥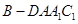 的体积.
的体积.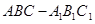 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则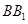 与平面
与平面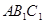 所成的角的大小为
所成的角的大小为
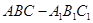 中,侧棱
中,侧棱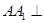 底面
底面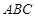 ,
,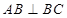 ,
,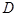 为
为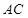 的中点,
的中点,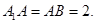
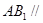 平面
平面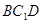 ;
; 作
作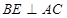 于点
于点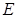 ,求证:直线
,求证:直线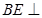 平面
平面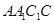
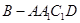 的体积为3,求
的体积为3,求 的长度
的长度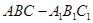 中,侧棱
中,侧棱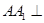 底面
底面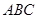 ,
,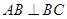 ,
, 为
为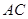 的中点,
的中点,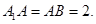
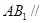 平面
平面 ;
;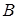 作
作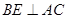 于点
于点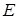 ,求证:直线
,求证:直线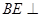 平面
平面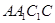
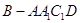 的体积为3,求
的体积为3,求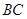 的长度
的长度