题目内容
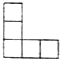
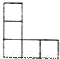
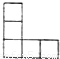
用若干个体积为1的正方体搭成一个几何体,其正(主)视图、侧(左)视图都是如图所示的图形,则这个几何体的最大体积是 .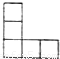
【答案】分析:由正视图和侧视图可知:该几何体的体积最大时,底层有9个小正方体,左上面有两个,共11个体积为1 的正方体.
据此可计算出答案.
解答: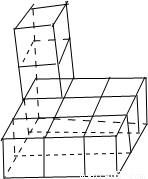 解:由正视图和侧视图可知:该几何体的体积最大时,底层有9个小正方体,左上面有两个,共11个体积为1 的正方体.
解:由正视图和侧视图可知:该几何体的体积最大时,底层有9个小正方体,左上面有两个,共11个体积为1 的正方体.
故V=11×1=11.
故答案为 11.
点评:由正视图和侧视图正确恢复原几何体是解决问题的关键.
据此可计算出答案.
解答:
 解:由正视图和侧视图可知:该几何体的体积最大时,底层有9个小正方体,左上面有两个,共11个体积为1 的正方体.
解:由正视图和侧视图可知:该几何体的体积最大时,底层有9个小正方体,左上面有两个,共11个体积为1 的正方体.故V=11×1=11.
故答案为 11.
点评:由正视图和侧视图正确恢复原几何体是解决问题的关键.

练习册系列答案
相关题目
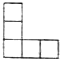 用若干个体积为1的正方体搭成一个几何体,其正(主)视图、侧(左)视图都是如图所示的图形,则这个几何体的最大体积是
用若干个体积为1的正方体搭成一个几何体,其正(主)视图、侧(左)视图都是如图所示的图形,则这个几何体的最大体积是