题目内容
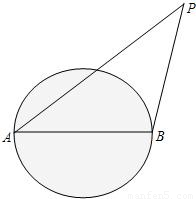
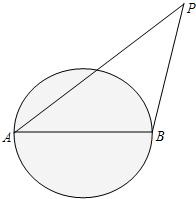 外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.
外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.(1)当α=30°,β=120°时,该外轮是否已进入我领海主权范围内?
(2)角α,β应满足什么关系时?就应向外轮发出警告,令其退出我海域.
分析:(1)取AB得中点O,连接OP根据α和β求得∴∠APB=30°进而可得AB=PB,利用余弦定理求得OP与18比较大小,进而得出结论.
(2)先利用正弦定理表示出AP和BP,进而设∠POB=θ,利用余弦定理求得AP2和BP2,根据AO=BO求得2PO2=AP2+BP2-2AO2,代入
-2×62<2×182求得α,β的关系
(2)先利用正弦定理表示出AP和BP,进而设∠POB=θ,利用余弦定理求得AP2和BP2,根据AO=BO求得2PO2=AP2+BP2-2AO2,代入
| 122sin2β+122sin2α |
| sin2(α+β) |
解答:解:(1)取AB得中点O,连接OP
∵∠α=30°,∠β=120°∴∠APB=30°,∴AB=PB=12
在三角形PBO中,OP2=62+122-2×6×12×cos120°=252
∴OP=6
<18
故该外轮已经进入我领海主权范围内.
(2)在三角形APB中,∠BAP=α,∠ABP=β,AB=12,由正弦定理得:
=
=
∴AP=
,BP=
在三角形POB与PBO中,设∠POB=θ∴AP2=AO2+PO2-2AO•POcos(π-θ),
∴BP2=BO2+PO2-2BO•POcosθ,AO=BO∴AP2+BP2=2AO2+2PO2
∴2PO2=AP2+BP2-2AO2,当PO<18时
得:
-2×62<2×182
即sin2α+sin2β<2sin2(α+β).
∵∠α=30°,∠β=120°∴∠APB=30°,∴AB=PB=12
在三角形PBO中,OP2=62+122-2×6×12×cos120°=252
∴OP=6
| 7 |
故该外轮已经进入我领海主权范围内.
(2)在三角形APB中,∠BAP=α,∠ABP=β,AB=12,由正弦定理得:
| PA |
| sinβ |
| PB |
| sinα |
| 12 |
| sin(α+β) |
∴AP=
| 12sinβ |
| sin(α+β) |
| 12sinα |
| sin(α+β) |
在三角形POB与PBO中,设∠POB=θ∴AP2=AO2+PO2-2AO•POcos(π-θ),
∴BP2=BO2+PO2-2BO•POcosθ,AO=BO∴AP2+BP2=2AO2+2PO2
∴2PO2=AP2+BP2-2AO2,当PO<18时
得:
| 122sin2β+122sin2α |
| sin2(α+β) |
即sin2α+sin2β<2sin2(α+β).
点评:本题主要考查了解三角形的实际应用.正弦定理和余弦定理是解三角形问题的常用公式,应熟练记忆.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)当
(1)当 (1)当
(1)当