题目内容
角α,β为锐角,向量
=(sinα,-2),
=(1,cosα),
⊥
(1)求sinα与cosα的值.
(2)若sin(α-β)=
,求β的值.
| m |
| n |
| m |
| n |
(1)求sinα与cosα的值.
(2)若sin(α-β)=
| ||
| 10 |
分析:(1)由题意可得
•
=sinα-2cosα=0,即 tanα=2,再由角α,β为锐角,利用同角三角函数的基本关系求出sinα与cosα的值.
(2)由-
<α-β<
,sin(α-β)=
,求得cos(α-β) 的值,再由cosβ=cos[(α-β)-α]利用两角差的余弦公式求得结果.
| m |
| n |
(2)由-
| π |
| 2 |
| π |
| 2 |
| ||
| 10 |
解答:解:(1)由题意可得
•
=sinα-2cosα=0,即 tanα=2,再由角α,β为锐角,sin2α+cos2α=1,
求得sinα=
,cosα=
.
(2)由于-
<α-β<
,sin(α-β)=
,∴cos(α-β)=
.
故cosβ=cos[(α-β)-α]=cos(α-β)cosα+sin(α-β)sinα=
×
+
×
=
,
∴β=
.
| m |
| n |
求得sinα=
2
| ||
| 5 |
| ||
| 5 |
(2)由于-
| π |
| 2 |
| π |
| 2 |
| ||
| 10 |
3
| ||
| 10 |
故cosβ=cos[(α-β)-α]=cos(α-β)cosα+sin(α-β)sinα=
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
∴β=
| π |
| 4 |
点评:本题主要考查两个向量的数量积公式的应用,同角三角函数的基本关系,两角差的余弦公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =(cosα,sinα),
=(cosα,sinα),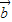 =(cosβ,sinβ),
=(cosβ,sinβ), =(
=( ,-
,- ).
). •
• =
= ,
, •
•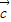 =
= ,求角2β-α的值;
,求角2β-α的值; =
= +
+ ,求tanα的值.
,求tanα的值.