题目内容
(1)已知命题p:π是无理数;命题q:3>5,判断“p∨q”,“p∧q”的真假.(2)画出一元二次不等式x+y-1>0表示的平面区域.
【答案】分析:(1)先判断命题p,q的真假,再根据真值表就可判断“p∧q”,“p∨q”的真假.
(2)作出不等式对应直线的图象,然后取特殊点代入不等式,判断不等式是否成立后得二元一次不等式表示的平面区域.
解答: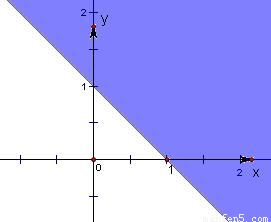 解:(1)∵π是无理数,∴命题p为真命题.
解:(1)∵π是无理数,∴命题p为真命题.
∵3>5不成立,∴命题q为假命题.
∴命题“p∨q”是真命题,命题“p∧q”是假命题.
(2)不等式x+y-1>0对应的函数x+y-1=0的图象是一条直线,取点(0,0),把该点的坐标代入不等式x+y-1>0不成立,说明不等式x+y-1>0表示的平面区域与点(0,0)异侧,
所以不等式x+y-1>0表示的平面区域在直线x+y-1=0的右上方,不含直线.
点评:(1)本题主要考查考查了简单命题和复合命题真假的判断,要熟记真值表.
(2)本题考查了二元一次不等式与平面区域,常用代特殊点验证法,当不等式对应的直线不过原点时,常取原点代入验证,过原点时,可任找一数值较小的点代入验证,此题是基础题.
(2)作出不等式对应直线的图象,然后取特殊点代入不等式,判断不等式是否成立后得二元一次不等式表示的平面区域.
解答:
 解:(1)∵π是无理数,∴命题p为真命题.
解:(1)∵π是无理数,∴命题p为真命题.∵3>5不成立,∴命题q为假命题.
∴命题“p∨q”是真命题,命题“p∧q”是假命题.
(2)不等式x+y-1>0对应的函数x+y-1=0的图象是一条直线,取点(0,0),把该点的坐标代入不等式x+y-1>0不成立,说明不等式x+y-1>0表示的平面区域与点(0,0)异侧,
所以不等式x+y-1>0表示的平面区域在直线x+y-1=0的右上方,不含直线.
点评:(1)本题主要考查考查了简单命题和复合命题真假的判断,要熟记真值表.
(2)本题考查了二元一次不等式与平面区域,常用代特殊点验证法,当不等式对应的直线不过原点时,常取原点代入验证,过原点时,可任找一数值较小的点代入验证,此题是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目