题目内容
向高为8m,底面边长为8m的倒置正四棱锥形的容器内注水,其速度为每分钟
m3,当水深为5m时,水面上升的速度是每分钟
m.
| 8 |
| 3 |
| 32 |
| 75 |
| 32 |
| 75 |
分析:利用平行线分线段成比例定理得到水面的半径与水高的关系;利用圆锥的体积公式求出水深与时间的函数关系;对水深求导数即为水上升的速度.
解答:解:设容器中水的体积在t分钟时为V,水深为h,V=
t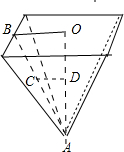
又V=
×CD2•h,
图知
=
⇒
=
⇒CD=
h,
∴V=
•(
h)2•h=
h3,
∴
t=
h3,⇒h=
,
∴h′=
×
×t-
.
h=5,t=
,h′=
.
∴当h=5米时,水面上升速度为
米/分.
故答案为:
.
| 8 |
| 3 |

又V=
| 1 |
| 3 |
图知
| CD |
| AD |
| BO |
| AO |
| CD |
| h |
| 4 |
| 8 |
| 1 |
| 2 |
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
∴
| 8 |
| 3 |
| 1 |
| 12 |
| 3 | 32t |
∴h′=
| 3 | 32 |
| 1 |
| 3 |
| 2 |
| 3 |
h=5,t=
| 125 |
| 32 |
| 32 |
| 75 |
∴当h=5米时,水面上升速度为
| 32 |
| 75 |
故答案为:
| 32 |
| 75 |
点评:本题考查圆锥的体积公式、平行线分线段成比例定理、对水深求导即为水上升的速度.

练习册系列答案
相关题目
 m3,当水深为5m时,水面上升的速度是每分钟________m.
m3,当水深为5m时,水面上升的速度是每分钟________m. m3,当水深为5m时,水面上升的速度是每分钟 m.
m3,当水深为5m时,水面上升的速度是每分钟 m.