题目内容
已知 的最小值为
的最小值为 ,则二项式
,则二项式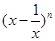 展开式中
展开式中 项的系数为( )
项的系数为( )
A. | B. | C. | D. |
A
解析试题分析:因为函数 的最小值为
的最小值为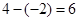 ,即
,即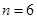 。展开式的通项公式为
。展开式的通项公式为 ,由
,由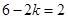 ,得
,得 ,所以
,所以 ,即
,即 项的系数为15,选A.
项的系数为15,选A.
考点:二项式定理,分段函数
点评:主要是考查了分段函数的最值,以及二项式定理的通项公式的运用,属于中档题。

练习册系列答案
相关题目
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这三项任务的不同选法有 ( )
| A.1260种 | B.2025种 | C.2520种 | D.5040种 |
4名学生被人大、清华、北大录取,若每所大学至少要录取1名,则共有不同的录取方法( )
| A.72种 | B.36种 | C.24种 | D.12种 |
有9 名翻译人员,其中6人只能做英语翻译,2人只能做韩语翻译,另外1人既可做英语翻译也可做韩语翻译.要从中选5人分别接待5个外国旅游团,其中两个旅游团需要韩语翻译,三个需要英语翻译,则不同的选派方法数为()
| A.900 | B.800 | C.600 | D.500 |
已知 ,则
,则 ( ).
( ).
A. | B. | C. | D. |
二项式 的展开式中含
的展开式中含 项的系数为( )
项的系数为( )
A. | B. | C. | D. |
今有甲乙丙三项任务,甲需2人承担,乙丙各需1人承担,现从10人中选派4人承担这三项任务,不同的选派方法有
| A.1260种 | B.2025种 | C.2520种 | D.5054种 |
 且
且 ,则乘积
,则乘积 等于( )
等于( )
A. | B. | C. | D. |
已知(1+ x)(1+x)5的展开式中x2的系数为5,则
x)(1+x)5的展开式中x2的系数为5,则 =
=
| A.-4 | B.-3 | C.-2 | D.-1 |