题目内容
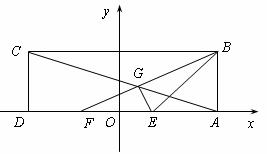
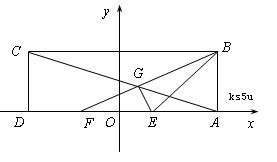
在矩形![]() 中,已知
中,已知![]() ,
,![]() ,E、F为
,E、F为![]() 的两个三等分点,
的两个三等分点,![]() 和
和![]() 交于点
交于点![]() ,
,![]() 的外接圆为⊙
的外接圆为⊙![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 中点
中点![]() 为坐标原点,建立如图所示的平面直角坐标系.
为坐标原点,建立如图所示的平面直角坐标系.
(1)求以F、E为焦点,![]() 和
和![]() 所在直线为准线的椭圆的方程;
所在直线为准线的椭圆的方程;
(2)求⊙![]() 的方程;
的方程;
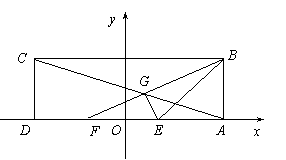 (3)设点
(3)设点![]() ,过点P作直线与⊙
,过点P作直线与⊙![]() 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数![]() 的取值范围.
的取值范围.
解(1)由已知,设椭圆方程为![]() ,
,
由于焦点![]() 的坐标为
的坐标为![]() ,它对应的准线方程为
,它对应的准线方程为 ![]() ,…………………2分
,…………………2分
所以![]() ,
,![]() ,于是
,于是 ![]() ,
,![]() ,
,
所以所求的椭圆方程为: ![]() . ……………………………………4分
. ……………………………………4分
(2) 由题意可知![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以直线![]() 和直线
和直线![]() 的方程分别为:
的方程分别为:![]() ,
,![]() ,
,
由![]() 解得
解得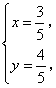 所以
所以![]() 点的坐标为
点的坐标为![]() .……………6分
.……………6分
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() , …………………………………………8分
, …………………………………………8分
所以⊙![]() 的圆心为
的圆心为![]() 中点
中点![]() ,半径为
,半径为![]() ,
,
所以⊙![]() 方程为
方程为 ![]() .………………………………………10分
.………………………………………10分
(3) 设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() 点的坐标为
点的坐标为![]() ,
,
因为点![]() 均在⊙
均在⊙![]() 上,所以
上,所以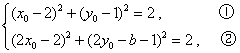 ,
,
由②-①×4,得![]() ,
,
所以点![]() 在直线
在直线![]() ,………………12分
,………………12分
又因为点![]() 在⊙
在⊙![]() 上,
上,
所以圆心![]() 到直线
到直线![]() 的距离
的距离
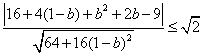
![]() , ………………………………14分
, ………………………………14分
即![]() ,
,
整理,得![]() ,即
,即![]() ,
,
 所以
所以![]() ,故
,故![]() 的取值范围为
的取值范围为![]() .………16分
.………16分
解法二:过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
设![]() 到直线
到直线![]() 的距离
的距离![]()
![]() ,则
,则
![]() ,
,
![]() ,
,
又因为![]()
所以![]()
![]() ,
,![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,![]() ;
;
解法三:因为![]() ,
,![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]() ,
,![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
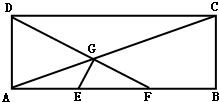 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系,
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系, 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: