题目内容
选做题A.在极坐标系中,圆C的极坐标方程为:ρ2+2ρcosθ=0,点P的极坐标为
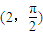 ,过点P作圆C的切线,则两条切线夹角的正切值是 .
,过点P作圆C的切线,则两条切线夹角的正切值是 .B.用0.618法对某一试验进行优选,因素范围是[2000,8000],则第二个试点x2是 .
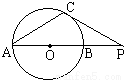
C.如图⊙o的直径AB=6cm,P是AB的延长线上一点,过点P作⊙o的切线,切点为C,连接AC,若∠CPA=30°,则PC= .
【答案】分析:A:把极坐标转化直角坐标方程,利用正切函数的二倍角公式求解即可.
B:由题知试验范围为[2000,8000],区间长度为6000,故可利用0.618法选取试点进行计算.
C:在圆中线段利用由切线定理求得∠OCP=Rt∠,进而利用直角三角形PCO中的线段,结合解直角三角形求得PC即可.
解答:解:A:圆C的极坐标方程为:ρ2+2ρcosθ=0,所以x2+y2+2x=0,圆心坐标(-1,0),半径为1,
点P的极坐标为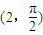 ,所以P的直角坐标为(0,2),
,所以P的直角坐标为(0,2),
过点P作圆C的切线,则两条切线夹角的正切值为:tanα=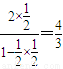 .
.
故答案为: .
.
B:解:根据0.618法,第一次试点加入量为
或8000-(8000-2000)×0.618=4292
故答案为:4292.
C:解:连接OC,
PC是⊙O的切线,
∴∠OCP=90°
∵∠CPA=30°,OC= =3,
=3,
∴tan30°= ,
,
即PC=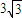 .
.
故答案为: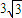 .
.
点评:A,考查极坐标与直角坐标的互化,二倍角公式的应用;B本题考查优先法的0.618法,属容易题,解答的关键是对黄金分割法-0.618法的了解.C此题考查的是直角三角形的性质、与圆有关的比例线段以及切线定理,属于基础题.
B:由题知试验范围为[2000,8000],区间长度为6000,故可利用0.618法选取试点进行计算.
C:在圆中线段利用由切线定理求得∠OCP=Rt∠,进而利用直角三角形PCO中的线段,结合解直角三角形求得PC即可.
解答:解:A:圆C的极坐标方程为:ρ2+2ρcosθ=0,所以x2+y2+2x=0,圆心坐标(-1,0),半径为1,
点P的极坐标为
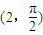 ,所以P的直角坐标为(0,2),
,所以P的直角坐标为(0,2),过点P作圆C的切线,则两条切线夹角的正切值为:tanα=
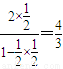 .
.故答案为:
 .
.B:解:根据0.618法,第一次试点加入量为
或8000-(8000-2000)×0.618=4292
故答案为:4292.
C:解:连接OC,
PC是⊙O的切线,
∴∠OCP=90°
∵∠CPA=30°,OC=
 =3,
=3,∴tan30°=
 ,
,即PC=
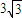 .
.故答案为:
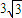 .
.点评:A,考查极坐标与直角坐标的互化,二倍角公式的应用;B本题考查优先法的0.618法,属容易题,解答的关键是对黄金分割法-0.618法的了解.C此题考查的是直角三角形的性质、与圆有关的比例线段以及切线定理,属于基础题.

练习册系列答案
相关题目
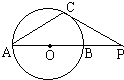 C.如图⊙o的直径AB=6cm,P是AB的延长线上一点,过点P作⊙o的切线,切点为C,连接AC,若∠CPA=30°,则PC=
C.如图⊙o的直径AB=6cm,P是AB的延长线上一点,过点P作⊙o的切线,切点为C,连接AC,若∠CPA=30°,则PC=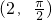 ,过点P作圆C的切线,则两条切线夹角的正切值是________.
,过点P作圆C的切线,则两条切线夹角的正切值是________.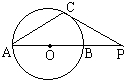 C.如图⊙o的直径AB=6cm,P是AB的延长线上一点,过点P作⊙o的切线,切点为C,连接AC,若∠CPA=30°,则PC=________.
C.如图⊙o的直径AB=6cm,P是AB的延长线上一点,过点P作⊙o的切线,切点为C,连接AC,若∠CPA=30°,则PC=________.