题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:由
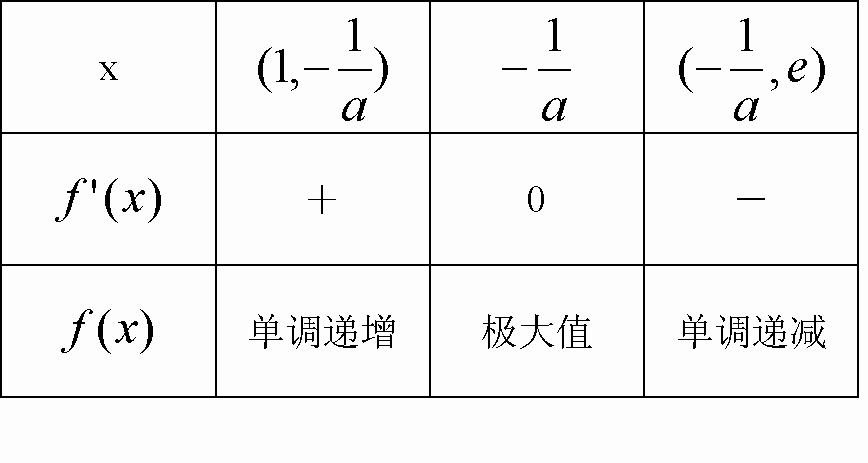
令 可得 又因为x∈(1,e)
所以,f(x)有极值3分 所以,实数 |
(2) |
解:由1可知f(x)的极大值为 又∵ 由 又∵ ∴当 当 |
(3) |
解:证明:由
令 令 又∵ ∴ ∵ ∴ ∵ ∴
∴ |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目