题目内容
设函数 ,数列{an}满足
,数列{an}满足
(1)求数列{an}的通项公式;
(2)令  ,试比较 Sn与
,试比较 Sn与 的大小,并加以证明.
的大小,并加以证明.
解:(1)∵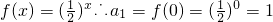 ,
,
又∵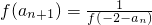
∴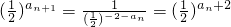 .…(2分)
.…(2分)
∴an+1=an+2即 an+1-an=2,∴数列{an}是首项为1,公差为 2 的等差数列
∴an=1+(n-1)×2=2n-1.…(5分)
(2)∵ ∴
∴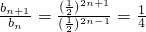 …(6分)
…(6分)
即数列{bn}是首项为 ,公比为
,公比为  的等比数列
的等比数列
∴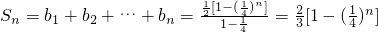 …(7分)
…(7分) =
=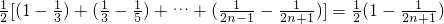 …(10分)
…(10分)
∴
故比较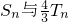 的大小,只需比较
的大小,只需比较 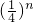 与
与 的大小即可 …(11分)
的大小即可 …(11分)
即只需比较 2n+1与4n的大小
∵4n=(1+3)n=1+Cn1•3+…≥3n+1>2n+1…(12分)
故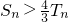 …(13分)
…(13分)
分析:解:(1)由已知, 可求a1=1,由
可求a1=1,由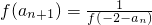 可得an+1-an=2,从而可得数列{an}是首项为1,公差为 2 的等差数列,从而可求通项公式
可得an+1-an=2,从而可得数列{an}是首项为1,公差为 2 的等差数列,从而可求通项公式
(2)由(1)可得 ,则有数列{bn}是等比数列,利用等比数列的前n项和公式可求Sn,利用裂项求和可求Tn,故比较
,则有数列{bn}是等比数列,利用等比数列的前n项和公式可求Sn,利用裂项求和可求Tn,故比较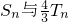 的大小,只需比较
的大小,只需比较 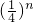 与
与 的大小即可,即只需比较 2n+1与4n的大小,利用二项展开式即可
的大小即可,即只需比较 2n+1与4n的大小,利用二项展开式即可
点评:本题主要考查了利用递推公式构造等差(等比)数列求解数列的通项公式,(2)综合考查了等比数列的前n项和公式及裂项求和的方法在求解数列的和中的应用,结局(2)的关键是要把所求的问题进行转换,结合二项展开式求解即可.
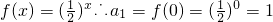 ,
,又∵
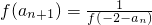
∴
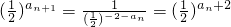 .…(2分)
.…(2分)∴an+1=an+2即 an+1-an=2,∴数列{an}是首项为1,公差为 2 的等差数列
∴an=1+(n-1)×2=2n-1.…(5分)
(2)∵
 ∴
∴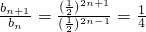 …(6分)
…(6分)即数列{bn}是首项为
 ,公比为
,公比为  的等比数列
的等比数列∴
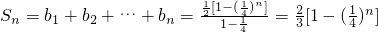 …(7分)
…(7分) =
=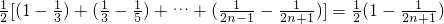 …(10分)
…(10分)∴

故比较
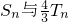 的大小,只需比较
的大小,只需比较 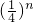 与
与 的大小即可 …(11分)
的大小即可 …(11分)即只需比较 2n+1与4n的大小
∵4n=(1+3)n=1+Cn1•3+…≥3n+1>2n+1…(12分)
故
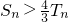 …(13分)
…(13分)分析:解:(1)由已知,
 可求a1=1,由
可求a1=1,由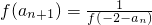 可得an+1-an=2,从而可得数列{an}是首项为1,公差为 2 的等差数列,从而可求通项公式
可得an+1-an=2,从而可得数列{an}是首项为1,公差为 2 的等差数列,从而可求通项公式(2)由(1)可得
 ,则有数列{bn}是等比数列,利用等比数列的前n项和公式可求Sn,利用裂项求和可求Tn,故比较
,则有数列{bn}是等比数列,利用等比数列的前n项和公式可求Sn,利用裂项求和可求Tn,故比较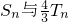 的大小,只需比较
的大小,只需比较 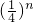 与
与 的大小即可,即只需比较 2n+1与4n的大小,利用二项展开式即可
的大小即可,即只需比较 2n+1与4n的大小,利用二项展开式即可点评:本题主要考查了利用递推公式构造等差(等比)数列求解数列的通项公式,(2)综合考查了等比数列的前n项和公式及裂项求和的方法在求解数列的和中的应用,结局(2)的关键是要把所求的问题进行转换,结合二项展开式求解即可.

练习册系列答案
相关题目
 ,数列{an}满足
,数列{an}满足
 ,试比较 Sn与
,试比较 Sn与 的大小,并加以证明.
的大小,并加以证明.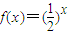 ,数列{an} 满足
,数列{an} 满足 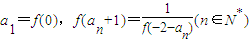
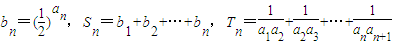 ,求 Sn与 Tn.
,求 Sn与 Tn. ,数列{an}满足
,数列{an}满足 .
. ,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列
,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列 ,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.
,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.