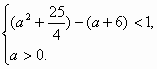题目内容
设x＝3是函数f(x)＝(x2＋ax＋b)e3－x(x∈R)的一个极值点．
(1)求a与b的关系式(用a表示b)，并求f(x)的单调区间；
(2)设a＞0，g(x)＝(a2＋
)ex．若存在ξ1，ξ2∈[0，4]使得|f(ξ1)－?g(ξ2)|＜1成立，求a的取值范围．
答案：
解析：
解析：
|
解：(1) 由 所以f(x)＝(x2＋ax－2a－3)e3－x， ＝－(x－3)(x＋a＋1)e3－x． 令 由于x＝3是f(x)的极值点， 故x1≠x2，即a≠－4． 当a＜－4时，x1＜x2． 故f(x)在(－∞，3]上为减函数，在[3，－a－1]上为增函数，在[－a－1，＋∞)上为减函数． 当a＞－4时，x1＞x2，故f(x)在(－∞，－a－1]上为减函数，在[－a－1，3]上为增函数，在[3，＋∞)上为减函数． (2)当a＞0时，－a－1＜0，故f(x)在[0，3]上为增函数，在[3，4]上为减函数，因此f(x)在[0，4]上的值域为[min{f(0)，f(4)}，f(3)]＝[－(2a＋3)e3，a＋6]． 而g(x)＝(a2＋ 注意到(a2＋ 故由假设知 解得0＜a＜ 故a的取值范围是(0， |
(x)＝－[x2＋(a－2)x＋b－a]e3－x．
)ex在[0，4]上为增函数，所以值域为[a2＋
，(a2＋
)2≥0，
．
练习册系列答案
备战中考寒假系列答案
相关题目
ex．若存在
、
∈[0，4]，使得|f(
)－g(
)|＜1成立，求a的取值范围．
ex．若存在
、
∈[0，4]，使得|f(
)－g(
)|＜1成立，求a的取值范围．
)ex，若存在ξ1，ξ2∈[0，4]，使得|f(ξ1)－g(ξ2)|＜1成立，求a的取值范围．
．若存在x1，x2∈[0，4]使得|f(x1)－g(x2)|＜1成立，求a的取值范围．