题目内容
(12分)
已知函数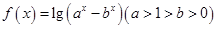 .
.
(1)求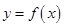 的定义域;
的定义域;
(2)在函数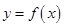 的图像上是否存在不同的两点,使过此两点的直线平行于
的图像上是否存在不同的两点,使过此两点的直线平行于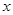 轴;
轴;
(3)当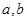 满足什么关系时,
满足什么关系时,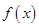 在
在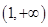 上恒取正值.
上恒取正值.
【答案】
(1)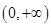 (2)函数
(2)函数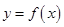 的图像上不存在不同的两点,使过这两点的直线平行于
的图像上不存在不同的两点,使过这两点的直线平行于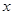 轴(3)
轴(3)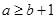
【解析】
试题分析:(1)由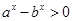 得
得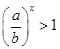 , 由已知
, 由已知 ,故
,故 ,
,
即函数 的定义域为
的定义域为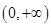 .
……4分
.
……4分
(2)设
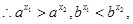 则
则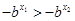 ,
,
故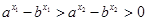 ,
,
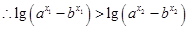 ,
,
即 .
.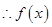 在
在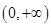 上为增函数.
上为增函数.
假设函数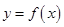 的图像上存在不同的两点
的图像上存在不同的两点 ,使直线
,使直线 平行于
平行于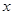 轴,即
轴,即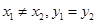 ,这与
,这与 是增函数矛盾.故函数
是增函数矛盾.故函数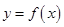 的图像上不存在不同的两点,使过这两点的直线平行于
的图像上不存在不同的两点,使过这两点的直线平行于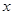 轴. ……8分
轴. ……8分
(3)由(2)知, 在
在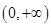 是增函数,
是增函数,
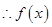 在
在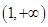 上也是增函数.
上也是增函数.
 当
当 时,
时,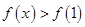 .
.
 只需
只需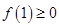 ,即
,即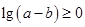 ,即
,即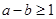 ,
,
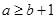 时,
时, 在
在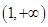 上恒取正值. ……12分
上恒取正值. ……12分
考点:本小题主要考查函数定义域的求解、函数性质的应用和恒成立问题的求解,考查学生对问题的转化能力和运算求解能力.
点评:定义域和值域必须写成集合或区间的形式,恒成立问题一般转化成最值问题解决.

练习册系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |