题目内容
(2013•梅州一模)设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的8高调函数,那么实数a的取值范围是
[-
,
]
| 2 |
| 2 |
[-
,
]
.| 2 |
| 2 |
分析:定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,画出函数f(x)的图象,可得8≥3a2-(-a2),从而可得结论.
解答:解:当x≥a2时f(x)=x-2a2,当0≤x<a2时f(x)=-x,再根据奇函数图象关于原点对称可作出f(x)的图象,如下图所示:
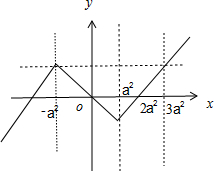
由f(x)为R上的8高调函数,知f(x+8)≥f(x)恒成立,
由图象得8≥3a2-(-a2),即a2≤2,解得-
≤a≤
.

由f(x)为R上的8高调函数,知f(x+8)≥f(x)恒成立,
由图象得8≥3a2-(-a2),即a2≤2,解得-
| 2 |
| 2 |
点评:本题考查基本初等函数的性质,考查学生的阅读能力,应用知识分析解决问题的能力,考查数形结合的能力,是一个新定义问题,注意对于条件中所给的一个新的概念,要注意理解.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目