题目内容
欢乐斗地主是一款QQ游戏,其规则:两名农民为一方合作对战一名地主,使用一副共54张的扑克牌,每人17张牌,剩余的3张归地主,只要有一人出完手中的牌,则此盘游戏结束.地主最先出完牌,则地主一方赢;两农民中的任何一人最先出完牌,则农民一方赢.输赢用欢乐豆结算:
(1)欢乐豆不足2000的人不能当地主.
(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).
甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为
,甲当农民时(不管谁当地主)最先出完牌的概率都为
;乙当地主时,最先出完牌的概率为
,乙当农民时(不管谁当地主)最先出完牌的概率为
.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )
(1)欢乐豆不足2000的人不能当地主.
(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).
甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为
| 1 |
| 2 |
| 7 |
| 30 |
| 13 |
| 30 |
| 1 |
| 6 |
分析:根据已知中甲当地主时,最先出完牌的概率为
,甲当农民时(不管谁当地主)最先出完牌的概率都为
;乙当地主时,最先出完牌的概率为
,乙当农民时(不管谁当地主)最先出完牌的概率为
.甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,分别计算甲当地主和当农民赢取欢乐豆的期望和丙当地主和当农民赢取欢乐豆的期望,比较后可得答案.
| 1 |
| 2 |
| 7 |
| 30 |
| 13 |
| 30 |
| 1 |
| 6 |
解答:解:∵甲当地主时,最先出完牌的概率为
,即甲当地主获胜的概率为
;由于乙欢乐豆只有500,此时甲可获得1500欢乐豆;而一旦输则损失2000欢乐豆,故甲当地主赢取欢乐豆的期望为:
×(-2000)+
×1500=-250
甲当农民时,甲乙无论谁先出完均能获胜,故甲当农民获胜的概率为
+
=
,故甲当农民赢取欢乐豆的期望为:
×1000+
×(-1000)=-200
由于当农民时的数学期望大于当地主时的数学期望,故甲不抢地主当
∵丙当地主时,获胜的概率为
,由于乙欢乐豆只有500,此时丙可获得1500欢乐豆;而一旦输则损失2000欢乐豆,故丙当地主赢取欢乐豆的期望为:
×(-2000)+
×1500=100
丙当农民时,丙乙无论谁先出完均能获胜,故丙当农民获胜的概率为
,故甲当农民赢取欢乐豆的期望为:
×1000+
×(-1000)=0
由于当农民时的数学期望小于当地主时的数学期望,故丙抢地主当
故选A
| 1 |
| 2 |
| 15 |
| 30 |
| 1 |
| 2 |
| 1 |
| 2 |
甲当农民时,甲乙无论谁先出完均能获胜,故甲当农民获胜的概率为
| 7 |
| 30 |
| 1 |
| 6 |
| 12 |
| 30 |
| 12 |
| 30 |
×1000+
| 18 |
| 30 |
由于当农民时的数学期望大于当地主时的数学期望,故甲不抢地主当
∵丙当地主时,获胜的概率为
| 18 |
| 30 |
| 12 |
| 30 |
| 18 |
| 30 |
丙当农民时,丙乙无论谁先出完均能获胜,故丙当农民获胜的概率为
| 1 |
| 2 |
| 1 |
| 2 |
×1000+
| 1 |
| 2 |
由于当农民时的数学期望小于当地主时的数学期望,故丙抢地主当
故选A
点评:本题考查的知识点是数学期望在实际中的应用,其中分别求出甲当地主和当农民赢取欢乐豆的期望和丙当地主和当农民赢取欢乐豆的期望,是解答的关键.

练习册系列答案
相关题目
 ,甲当农民时(不管谁当地主)最先出完牌的概率都为
,甲当农民时(不管谁当地主)最先出完牌的概率都为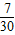 ;乙当地主时,最先出完牌的概率为
;乙当地主时,最先出完牌的概率为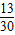 ,乙当农民时(不管谁当地主)最先出完牌的概率为
,乙当农民时(不管谁当地主)最先出完牌的概率为 .现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )
.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )