题目内容
9.在梯形ABCD中,AB⊥BC,AD∥BC,BC=2AD=2AB=4,将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为$\frac{40π}{3}$.分析 画出几何体的直观图,利用已知条件,求解几何体的体积即可得到答案.
解答 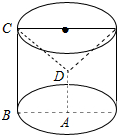 解:由题意可知几何体的直观图如图:
解:由题意可知几何体的直观图如图:
旋转体是底面半径为2,高为4的圆柱,挖去一个相同底面高为2的倒圆锥,
几何体的体积为:$π•{2}^{2}•4-\frac{1}{3}π•{2}^{2}•2$=$\frac{40π}{3}$.
故答案为:$\frac{40π}{3}$.
点评 本题考查几何体的体积的求法,考查空间想象能力以及计算能力.画出几何体的直观图是解题的关键,是中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
19.定义行列式运算:$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,函数f(x)=$|\begin{array}{l}{\sqrt{3}}&{cos2x}\\{1}&{sin2x}\end{array}|$,则要得到函数f(x)的图象,只需将y=2cos2x的图象( )( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
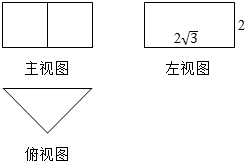 若一个三棱柱的三视图如图所示,主视图与左视图均为矩形,俯视图为正三角形,求这个三棱柱的底面边长与高.
若一个三棱柱的三视图如图所示,主视图与左视图均为矩形,俯视图为正三角形,求这个三棱柱的底面边长与高. 已知数列{an},观察程序框图,若k=5时,分别有S=25.
已知数列{an},观察程序框图,若k=5时,分别有S=25.