题目内容
(本小题满分12分)已知二次函数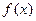 满足条件
满足条件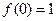 ,及
,及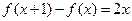 .
.
(1)求函数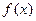 的解析式;
的解析式;
(2)在区间[-1,1]上,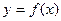 的图像恒在
的图像恒在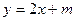 的图像上方,试确定实数m的取值范围;
的图像上方,试确定实数m的取值范围;
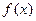 满足条件
满足条件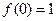 ,及
,及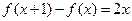 .
.(1)求函数
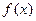 的解析式;
的解析式;(2)在区间[-1,1]上,
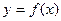 的图像恒在
的图像恒在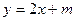 的图像上方,试确定实数m的取值范围;
的图像上方,试确定实数m的取值范围;(1) (2)
(2)
 (2)
(2)
解:(1)令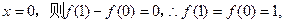
∴二次函数图像的对称轴为 .∴可令二次函数的解析式为
.∴可令二次函数的解析式为 .
.
由
∴二次函数的解析式为
(2) 在
在 上恒成立
上恒成立 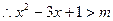 在
在 上恒成立
上恒成立
令 ,则
,则 在
在 上单调递减 ∴
上单调递减 ∴ .
.
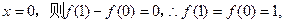
∴二次函数图像的对称轴为
 .∴可令二次函数的解析式为
.∴可令二次函数的解析式为 .
.由

∴二次函数的解析式为

(2)
 在
在 上恒成立
上恒成立 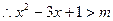 在
在 上恒成立
上恒成立令
 ,则
,则 在
在 上单调递减 ∴
上单调递减 ∴ .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
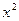 -ax-3(
-ax-3(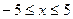 )
) f(x)=x2+ax+b,满足f(1)=0,f(2)
f(x)=x2+ax+b,满足f(1)=0,f(2) =0,则f(-1)= ▲ .
=0,则f(-1)= ▲ .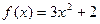 在区间
在区间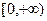 上是增函数.
上是增函数.
 与
与
 且
且 在区间
在区间 上都是减函数,则
上都是减函数,则 的取值范围是( )
的取值范围是( )


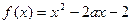 在[ 1,+∞)上单调递增”的( )
在[ 1,+∞)上单调递增”的( )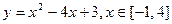 ,则
,则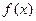 的最小值和最大值为__ __和 ___
的最小值和最大值为__ __和 ___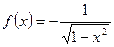 的单调递增区间为 .
的单调递增区间为 .