题目内容
设函数f(x)=cos2ωx其中0<ω<2.(I)设
 ,求f(x)的单调增区间;
,求f(x)的单调增区间;(II)若函数f(x)的图象的一条对称轴为
 ,求ω的值.
,求ω的值.
【答案】分析:(I)把ω的值代入函数解析式后,利用二倍角的余弦函数公式化简得到一个关于x的余弦函数,找出余弦函数的单调递增区间,即为函数f(x)的单调增区间;
(II)根据二倍角的余弦函数公式化简已知的函数解析式,因为函数f(x)的图象的一条对称轴为 ,把
,把 代入函数解析式,得到的函数值f(
代入函数解析式,得到的函数值f(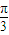 )为函数的最值,从而得到
)为函数的最值,从而得到 ,根据余弦函数的图象与性质得
,根据余弦函数的图象与性质得
,由k为正整数且0<ω<2,即可得出ω的值.
解答:解:(I)当 时,
时, ,(2分)
,(2分)
∴f(x)的单调增区间是(2kπ-π,2kπ)(k∈Z);(5分)
(II)化简得: ,
,
∵函数f(x)的图象的一条对称轴为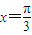 ,
,
∴ 取最值,
取最值,
∴ ,(8分)
,(8分)
∴ (k∈Z),
(k∈Z),
∴ ,(10分)
,(10分)
∵0<ω<2,
∴ .(12分)
.(12分)
点评:此题考查了二倍角的余弦函数公式,余弦函数的单调性及对称性,灵活运用二倍角的余弦函数公式,熟练掌握余弦函数的图象与性质是解本题的关键.
(II)根据二倍角的余弦函数公式化简已知的函数解析式,因为函数f(x)的图象的一条对称轴为
 ,把
,把 代入函数解析式,得到的函数值f(
代入函数解析式,得到的函数值f(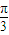 )为函数的最值,从而得到
)为函数的最值,从而得到 ,根据余弦函数的图象与性质得
,根据余弦函数的图象与性质得
,由k为正整数且0<ω<2,即可得出ω的值.
解答:解:(I)当
 时,
时, ,(2分)
,(2分)∴f(x)的单调增区间是(2kπ-π,2kπ)(k∈Z);(5分)
(II)化简得:
 ,
,∵函数f(x)的图象的一条对称轴为
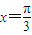 ,
,∴
 取最值,
取最值,∴
 ,(8分)
,(8分)∴
 (k∈Z),
(k∈Z),∴
 ,(10分)
,(10分)∵0<ω<2,
∴
 .(12分)
.(12分)点评:此题考查了二倍角的余弦函数公式,余弦函数的单调性及对称性,灵活运用二倍角的余弦函数公式,熟练掌握余弦函数的图象与性质是解本题的关键.

练习册系列答案
相关题目