题目内容
若自然数n使得作竖式加法 均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )
均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )
 均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )
均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )| A.27 | B.36 | C.39 | D.48 |
D
分析:本题是个新定义的题,由定义知,符合条件的良数有三个,一位数,二位数,三位数,且个数数字只能是0,1,2,非个位数字只能是0,1,2,3(首位不为0),分三类计数,选出正确选项
解答:解:如果n是良数,则n的个位数字只能是0,1,2,非个位数字只能是0,1,2,3(首位不为0),
而小于1000的数至多三位,
一位的良数有0,1,2,共3个
二位的良数个位可取0,1,2,十位可取1,2,3,共有3×3=9个
三位的良数个位可取0,1,2,十位可取0,1,2,3,百位可取1,2,3,共有3×4×3=36个.
综上,小于1000的“良数”的个数为3+9+36=48个
故选D
点评:本题考查排列组合及简单计数问题,解题的关键是理解新定义,新定义型题,是近几年高考中出现频率较高的题,此类题的求解理解定义是入手的关键,考查理解能力
解答:解:如果n是良数,则n的个位数字只能是0,1,2,非个位数字只能是0,1,2,3(首位不为0),
而小于1000的数至多三位,
一位的良数有0,1,2,共3个
二位的良数个位可取0,1,2,十位可取1,2,3,共有3×3=9个
三位的良数个位可取0,1,2,十位可取0,1,2,3,百位可取1,2,3,共有3×4×3=36个.
综上,小于1000的“良数”的个数为3+9+36=48个
故选D
点评:本题考查排列组合及简单计数问题,解题的关键是理解新定义,新定义型题,是近几年高考中出现频率较高的题,此类题的求解理解定义是入手的关键,考查理解能力

练习册系列答案
相关题目
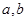 分别为2,3时,最后输出的
分别为2,3时,最后输出的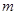 的值是________.
的值是________.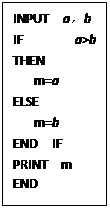




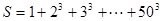 的值,并写出程序。
的值,并写出程序。

 则可以输出的函数是
则可以输出的函数是 =__________
=__________