题目内容

对于数列{a_n}满足a1=1，

a2k

a2k-1

=2，

a2k+1

a2k

=3(k∈N+)，则其前100项的和S₁₀₀=

(650-1)

．

分析：由条件可得数列{a_n}奇数项组成以1为首项，6为公比的等比数列，偶数项组成以2为首项，6为公比的等比数列，理由等比数列的求和公式，即可求得结论．

解答：解：∵

a2k

a2k-1

=2，

a2k+1

a2k

=3
∴

a2k+1

a2k-1

=6，

a2k+2

a2k

=6
∵a₁=1，a₂=2
∴数列{a_n}奇数项组成以1为首项，6为公比的等比数列，偶数项组成以2为首项，6为公比的等比数列
∴前100项的和S₁₀₀=

1-650

1-6

2(1-650)

1-6

(650-1)
故答案为：

(650-1)

点评：本题考查数列的求和，解题的关键是确定数列{a_n}奇数项组成以1为首项，6为公比的等比数列，偶数项组成以2为首项，6为公比的等比数列．

练习册系列答案

名校百分金卷系列答案

随堂大考卷系列答案

小学生每日20分钟系列答案

口算题卡加应用题专项沈阳出版社系列答案

相关题目

（2011•西城区二模）数列{a_n}满足a₁=1，an+1=

n-λ

n+1

an，其中λ∈R，n=1，2，…．给出下列命题：
①?λ∈R，对于任意i∈N^*，a_i＞0；
②?λ∈R，对于任意i≥2（i∈N^*），a_ia_i+1＜0；
③?λ∈R，m∈N^*，当i＞m（i∈N^*）时总有a_i＜0．
其中正确的命题是

①③

．（写出所有正确命题的序号）

如果存在常数a使得数列{a_n}满足：若x是数列{a_n}中的一项，则a-x也是数列{a_n}中的一项，称数列{a_n}为“兑换数列”，常数a是它的“兑换系数”．
（1）若数列：1，2，4，m（m＞4）是“兑换系数”为a的“兑换数列”，求m和a的值；
（2）已知有穷等差数列b_n的项数是n₀（n₀≥3），所有项之和是B，求证：数列b_n是“兑换数列”，并用n₀和B表示它的“兑换系数”；
（3）对于一个不少于3项，且各项皆为正整数的递增数列{c_n}，是否有可能它既是等比数列，又是“兑换数列”？给出你的结论并说明理由．

（2013•内江一模）对于函数f（x），若存在x₀∈R，使f（x₀）=x₀成立，则称x₀为f（x）的不动点．如果函数f(x)=

x2+a

bx-c

有且仅有两个不动点0、2．
（1）求b，c满足的关系式；
（2）若c=2时，相邻两项和不为零的数列{a_n}满足4Snf(

)=1（S_n是数列{a_n}的前n项和），求证：-

对于数列{a_n}满足 $数学公式$ ，则其前100项的和S₁₀₀=________．

对于数列{an}满足，则其前100项的和S100=________．

试题分类

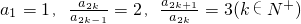对于数列{a_n}满足 $数学公式$ ，则其前100项的和S₁₀₀=________．