题目内容
(理)在锐角△ABC中,“A>B”是“sin2A>sin2B”的
既不充分又不必要
既不充分又不必要
条件.分析:在锐角△ABC中,A>B则π>2A>2B>0,根据正弦函数在这个区间上不是单调函数,故不一定推出sin2A>sin2B.当sin2A>sin2B时,不能判断两个角之间的关系,故不能推出A>B.
解答:解:在锐角△ABC中,“A>B”则π>2A>2B>0,根据正弦函数在这个区间上不是单调函数,
故不一定推出“sin2A>sin2B”.
当sin2A>sin2B时,不能判断两个角之间的关系,故不能推出A>B
∴前者是后者的既不充分又不必要条件,
故答案为:既不充分又不必要条件
故不一定推出“sin2A>sin2B”.
当sin2A>sin2B时,不能判断两个角之间的关系,故不能推出A>B
∴前者是后者的既不充分又不必要条件,
故答案为:既不充分又不必要条件
点评:本题考查正弦函数的单调性,本题解题的关键是看出二倍角的范围,理解在这个区间上正弦函数不是单调函数,本题是一个基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
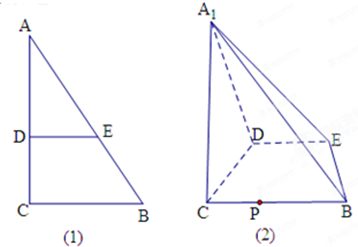 (理)如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
(理)如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).