题目内容
已知i,m,n是正整数,且1<i≤m<n.
(1)证明: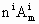 <
<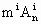 ;
;
(2)证明:(1+m)n>(1+n)m.
答案:
解析:
解析:
|
(1)证明:对于1<i≤m,有: 同理有: (2)由二项式定理,有:(1+m)n= |

练习册系列答案
相关题目
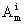 =m(m-1)…(m-i+1),
=m(m-1)…(m-i+1),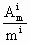 =
=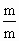 ·
·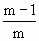 …
…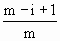 .
.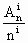 =
=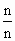 ·
·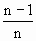 …
…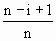 .因为m<n且
.因为m<n且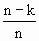 >
>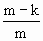 (k=1,2,…,i-1),所以
(k=1,2,…,i-1),所以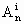 >ni
>ni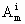 .
.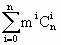 ,(1+n)m=
,(1+n)m=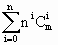 ,由(1)知mi
,由(1)知mi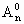 =n0
=n0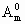 =1,m
=1,m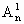 =n
=n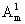 =mn,mi
=mn,mi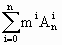 >
>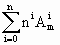 .即(1+m)n>(1+n)m.
.即(1+m)n>(1+n)m. IA)∪(
IA)∪(