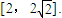题目内容
已知圆系C:(x-t)2+(y-t2)2=t2+(t2-| 1 |
| 2 |
①不论t取何实数,圆心C始终落在曲线y2=x上;
②不论t取何实数,弦MN的长为定值1;
③不论t取何实数,圆系C的所有圆都与直线y=
| 1 |
| 2 |
④式子
| m |
| n |
| n |
| m |
| 2 |
其中真命题的序号是
分析:分析圆的方程特点,圆心C(t,t2)在直线 y=x2上;由弦长公式求弦MN的长;由圆心到直线的距离和半径
作比较,判断直线和圆的位置关系;先求出m和n的值,有基本不等式可证
+
≥2,由余弦定理求出
cosA,由三角形的面积可求 sinA,再运sinA+cosA≤
,可得
+
≤2
,从而得出结论.
作比较,判断直线和圆的位置关系;先求出m和n的值,有基本不等式可证
| m |
| n |
| n |
| m |
cosA,由三角形的面积可求 sinA,再运sinA+cosA≤
| 2 |
| m |
| n |
| n |
| m |
| 2 |
解答:解:由圆C的方程知,圆心C(t,t2)在曲线y=x2上,故①不正确.
由弦长公式得:弦MN的长为 2
=2
=2
=1,故②正确.
圆心C(t,t2)到直线y=
的距离等于|t2-
|,而半径为
,二者不一定相等,
故③不正确.
在圆C方程令y=0,可得 x2-2t2x+t4-
=0,∴x=t2+
或 x=t2-
,
即 M(t2+
,0),N(t2-
,0),由圆C方程知A(0,
),
∴|AM|=m=
,|AN|=n=
,
由基本不等式得
+
≥2(当且仅当m=n时等号成立),
△AMN中,由余弦定理得 1=m2+n2-2mncosA,∴cosA=
,
△AMN的面积为
•m•n•sinA=
×1×
,∴sinA=
,
∵sinA+cosA=
≤
,∴
+
=
≤2
,
即 2
≥
+
≥2,故④正确.
故答案为 ②④.
由弦长公式得:弦MN的长为 2
| r2-d2 |
[t2+(t2-
|
|
圆心C(t,t2)到直线y=
| 1 |
| 2 |
| 1 |
| 2 |
t2+(t2-
|
故③不正确.
在圆C方程令y=0,可得 x2-2t2x+t4-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
即 M(t2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|AM|=m=
(t2+
|
(t2-
|
| 1 |
| 4 |
由基本不等式得
| m |
| n |
| n |
| m |
△AMN中,由余弦定理得 1=m2+n2-2mncosA,∴cosA=
| m2+n2-1 |
| 2mn |
△AMN的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2mn |
∵sinA+cosA=
| m2+n2 |
| 2mn |
| 2 |
| m |
| n |
| n |
| m |
| m2+n2 |
| mn |
| 2 |
即 2
| 2 |
| m |
| n |
| n |
| m |
故答案为 ②④.
点评:本题综合考查圆系方程的性质,重点考查圆心的坐标特征,点到直线的距离公式、弦长公式、直线和圆的
位置关系以及余弦定理的应用,并运用sinA+cosA≤
这个结论,属于中档题.
位置关系以及余弦定理的应用,并运用sinA+cosA≤
| 2 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
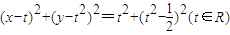 ,圆C过y轴上的定点A,线段MN是圆C在x轴上截得的弦,设|AM|=m,|AN|=n.对于下列命题:
,圆C过y轴上的定点A,线段MN是圆C在x轴上截得的弦,设|AM|=m,|AN|=n.对于下列命题: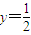 相切;
相切;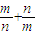 的取值范围是
的取值范围是