题目内容
已知函数 的图象与
的图象与 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于 ,则为得到函数
,则为得到函数 的图象可以把函数
的图象可以把函数 的图象上所有的点( )
的图象上所有的点( )
 的图象与
的图象与 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于 ,则为得到函数
,则为得到函数 的图象可以把函数
的图象可以把函数 的图象上所有的点( )
的图象上所有的点( )A.向右平移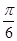 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
B.向右平移 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
C.向左平移 ,再将所得图象上所有的点的纵坐标变为原来的 ,再将所得图象上所有的点的纵坐标变为原来的 倍 倍 |
D.向左平移 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
A
分析:先利用两角差的正弦公式将函数f(x)=sinωx-
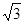 cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断
cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断解答:解:∵f(x)=sinωx-
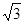 cosωx=2(
cosωx=2(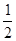 sinωx-
sinωx- 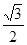 cosωx)=2sin(ωx-
cosωx)=2sin(ωx-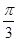 )
)又∵f(x)的图象与x轴的两个相邻交点的距离等于
 ,
,∴函数f(x)的最小正周期为T=2×
 =π
=π∴2π /ω =π,ω=2
∴f(x)=2sin(2x-
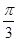 )=2sin2(x-
)=2sin2(x-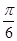 ),
),∴为得到函数y=f(x)的图象可以把函数y=sin2x的图象上所有的点向右平移
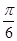 ,得y=sin2(x-
,得y=sin2(x-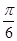 )的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-
)的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-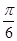 )的图象
)的图象故选A.
点评:本题考查了三角变换公式的应用,三角函数的图象和性质,周期公式,三角函数图象变换的方法等基础知识

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
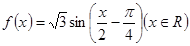 的最小正周期为
的最小正周期为



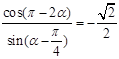 ,则
,则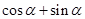 等于( )
等于( )



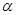 的始边为
的始边为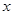 轴的非负半轴,顶点为坐标原点,点
轴的非负半轴,顶点为坐标原点,点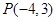 为其终边上一点,
为其终边上一点,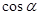 的值为
的值为
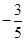


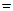
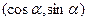 ,b
,b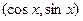 ,
,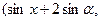
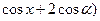 ,其中
,其中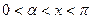 .
.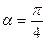 ,求函数
,求函数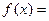 b·c的最小值及相应的
b·c的最小值及相应的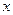 的值;
的值;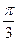 ,且a⊥c,求
,且a⊥c,求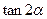 的值.
的值.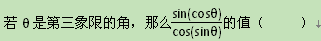
 ,
, .
. 的值;
的值;  的值.
的值.
 的最小正周期为2,则实数
的最小正周期为2,则实数
 的面积
的面积 ,则角
,则角 的大小为( )
的大小为( )