题目内容

如图，菱形ABCD的边长为1，∠ABC=60°，E、F分别为AD、CD的中点，则
BE
•
BF
=
 
．
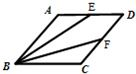
精英家教网
分析：把要求的式子化为（
BA
+
1
2
AD
）•（
BC
+
1
2
CD
），再利用两个向量的数量积的定义可得要求的式子等于
 1×1cos60°+
1
2
×1×1+
1
2
×1×1+
1
4
  1×1cos60°，运算求得结果．
解答：解：
BE
•
BF
=（
BA
+
1
2
AD
）•（
BC
+
1
2
CD
）=
BA
•
BC
+
1
2
 
BA
•
CD
+
1
2
 
AD
•
BC
+
1
4
 
AD
•
CD

=1×1cos60°+
1
2
×1×1+
1
2
×1×1+
1
4
1×1cos60°=
3
2
+
1
8
=
13
8
，
故答案为 
13
8
．
点评：本题考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，把要求的式子化为
（
BA
+
1
2
AD
）•（
BC
+
1
2
CD
），是解题的关键．
练习册系列答案
相关题目
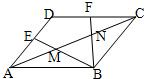精英家教网如图，菱形ABCD的边长为1，有∠D=120°，点E、F分别是AD、DC的中点，BE、BF分别与AC交于点M、N．
（1）求AC的值．
（2）求MN的值．
（2011•西城区二模）如图，菱形ABCD的边长为6，∠BAD=60°，AC∩BD=O．将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=3
2
．
（Ⅰ）求证：OM∥平面ABD；
（Ⅱ）求证：平面ABC⊥平面MDO；
（Ⅲ）求三棱锥M-ABD的体积．
如图，菱形ABCD的边长为4，∠BAD=60°，AC∪BD=O．将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=2
2
．
（1）求证：OM∥平面ABD；
（2）求证：平面DOM⊥平面ABC；
（3）求三棱锥B-DOM的体积．
如图，菱形ABCD的边长为4，∠BAD=60°，AC∩BD=O．将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=2
2
．
（1）求证：OM∥平面ABD；
（2）求证：平面DOM⊥平面ABC；
（3）求二面角D-AB-O余弦值．
如图，菱形ABCD的边长为2，∠A=60°，M为DC的中点，若N为菱形内任意一点（含边界），则
AM
•
AN
的最大值为
9
9
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网