题目内容
双曲线
的渐近线与圆
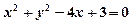的位置关系为
| A．相切 | B．相交但不经过圆心 | C．相交且经过圆心 | D．相离 |
A
解析
练习册系列答案
相关题目
的焦点到渐近线的距离为（ ）
C 
D 1
的准线与
轴交于点
.过点
两点，.点
在抛物线对称轴上,且
.则
的取值范围是 
抛物线x2=－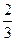
y的焦点的纵坐标与它的通径的比是
| A．4 | B．－4 | C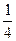． | D．－ |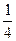
题目内容
双曲线的渐近线与圆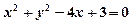的位置关系为
| A．相切 | B．相交但不经过圆心 | C．相交且经过圆心 | D．相离 |
A
解析
抛物线x2=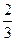－y的焦点的纵坐标与它的通径的比是
| A．4 | B．－4 | C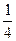． | D．－ |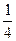
过椭圆左焦点F1和一个顶点B，则该椭圆的离心率为 ( )
的左、右焦点分别是
、
，过点
、
．若△
为正三角形，则该双曲线的离心率为 
，双曲线
，抛物线
(其中
的离心率分别为
，则
的值为 ( ) 
与
有关
的两个焦点，A和B是以O为圆心，以|OF1|为半径的圆与该双曲线左支的两个交点，且
是等边三角形，则双曲线的离心率为 （ ）
