Question

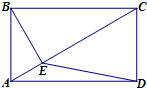
（2013•广东）（几何证明选讲选做题）
如图，在矩形ABCD中，AB=

3

，BC=3，BE⊥AC，垂足为E，则ED=

21

2

．

Answer 1

分析：由矩形ABCD，得到三角形ABC为直角三角形，由AB与BC的长，利用勾股定理求出AC的长，进而得到AB为AC的一半，利用直角三角形中直角边等于斜边的一半得到∠ACB=30°，且利用射影定理求出EC的长，在三角形ECD中，利用余弦定理即可求出ED的长．

解答：解：∵矩形ABCD，∴∠ABC=90°，
∴在Rt△ABC中，AB=

3

，BC=3，根据勾股定理得：AC=2

3

，
∴AB=

1

2

AC，即∠ACB=30°，EC=

BC2

AC

=

3 3

2

，
∴∠ECD=60°，
在△ECD中，CD=AB=

3

，EC=

3 3

2

，
根据余弦定理得：ED²=EC²+CD²-2EC•CDcos∠ECD=

27

4

+3-

9

2

=

21

4

，
则ED=

21

2

．
故答案为：

21

2

点评：此题考查了余弦定理，勾股定理，直角三角形的性质，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．