题目内容
过椭圆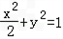 的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.
的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.
(1)求k的值;
(2)设C(﹣2,0),求tan∠ACB.
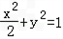 的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.
的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.(1)求k的值;
(2)设C(﹣2,0),求tan∠ACB.
解:(1)由椭圆方程,a= 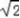 ,b=1,c=1,则点F为(﹣1,0).
,b=1,c=1,则点F为(﹣1,0).
直线AB方程为y=k(x+1),代入椭圆方程,得(2k2+1)x2+4k2x+2k2﹣2=0.①
设A(x1,y1),B(x2,y2),M(x0,y0),
则 x0=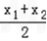 =﹣
=﹣ ,y0=k(x0+1)=
,y0=k(x0+1)=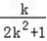 ,
,
由点M在直线x+2y=0上,知﹣2k2+2k=0,
∵k≠0, ∴k=1.
(2)将k=1代入①式,得3x2+4x=0,不妨设x1>x2,则x1=0,x2=﹣ ,
,
记α=∠ACF,β=∠BCF,则 tanα=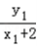 =
=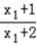 =
=  ,tanβ=﹣
,tanβ=﹣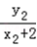 =﹣
=﹣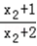 =
=  ,
,
∴α=β, ∴tan∠ACB=tan2α= =
= .
.
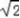 ,b=1,c=1,则点F为(﹣1,0).
,b=1,c=1,则点F为(﹣1,0).直线AB方程为y=k(x+1),代入椭圆方程,得(2k2+1)x2+4k2x+2k2﹣2=0.①
设A(x1,y1),B(x2,y2),M(x0,y0),
则 x0=
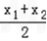 =﹣
=﹣ ,y0=k(x0+1)=
,y0=k(x0+1)=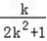 ,
,由点M在直线x+2y=0上,知﹣2k2+2k=0,
∵k≠0, ∴k=1.
(2)将k=1代入①式,得3x2+4x=0,不妨设x1>x2,则x1=0,x2=﹣
 ,
,记α=∠ACF,β=∠BCF,则 tanα=
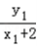 =
=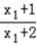 =
=  ,tanβ=﹣
,tanβ=﹣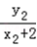 =﹣
=﹣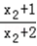 =
=  ,
,∴α=β, ∴tan∠ACB=tan2α=
 =
= .
. 
练习册系列答案
相关题目
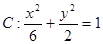 的右焦点F作斜率为
的右焦点F作斜率为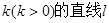 与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足: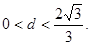
 的取值范围。
的取值范围。 的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.
的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.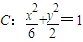 的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:
的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足: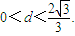
 的取值范围.
的取值范围.