题目内容
设函数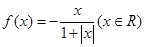 ,区间
,区间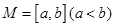 ,集合
,集合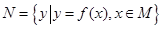 ,则使M=N成立的实数对
,则使M=N成立的实数对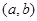 有( )
有( )
A.0个 B.1个 C.2个 D.无数多个
【答案】
A
【解析】
试题分析:解:∵x∈R, ,∴f(x)为奇函数,
,∴f(x)为奇函数, ∴f(x)在R上单调递减,∵函数在区间[a,b]上的值域也为[a,b],则f(a)=b,f(b)=a,即
∴f(x)在R上单调递减,∵函数在区间[a,b]上的值域也为[a,b],则f(a)=b,f(b)=a,即
 解得a=0,b=0,∵a<b,使M=N成立的实数对 (a,b)有0对,故选A
解得a=0,b=0,∵a<b,使M=N成立的实数对 (a,b)有0对,故选A
考点:集合相等,函数奇偶性与单调性
点评:本题考查的知识点是集合相等,函数奇偶性与单调性的综合应用,其中根据函数的性质,构造出满足条件的关于a,b的方程组,是解答本题的关键

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
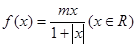 ,区间
,区间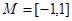 ,集合
,集合 ,则使
,则使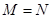 成立的实数
成立的实数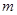 的个数为
的个数为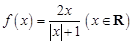 ,区间
,区间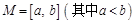 ,集合
,集合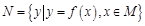 ,则使
,则使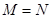 成立的实数对
成立的实数对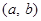 有 ( )
有 ( ) ,区间
,区间 ,集合
,集合 ,则使
,则使 成立的实数对
成立的实数对 有 ▲ 对.
有 ▲ 对.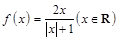 ,区间
,区间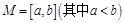 ,集合
,集合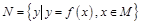 ,则使
,则使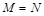 成立的实数对
成立的实数对 有
( )
有
( )