题目内容
若命题“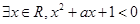 ”是真命题,则实数
”是真命题,则实数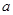 的取值范围为 .
的取值范围为 .
 .
.
解析试题分析:由题意可知,不等式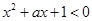 有解,∴
有解,∴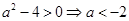 或
或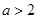 ,故实数
,故实数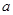 的取值范围是
的取值范围是 .
.
考点:一元二次不等式.

练习册系列答案
相关题目
若关于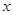 的不等式
的不等式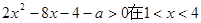 内有解,则实数
内有解,则实数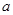 的取值范围是
的取值范围是
A. | B.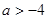 | C. | D. |
设函数f(x)=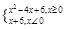 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )
| A.(-3,1)∪(3,+∞) | B.(-3,1)∪(2,+∞) |
| C.(-1,1)∪(3,+∞) | D.(-∞,-3)∪(1,3) |
在下列函数中,当x取正数时,最小值为2的是( )
A.y=x+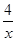 | B.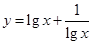 |
C. | D.y=x2-2x+3 |
若不等式ax2+bx+2>0的解集是{x| - < x <
< x < },则a + b的值为 ( )
},则a + b的值为 ( )
| A.-10 | B.-14 | C.10 | D.14 |
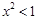 的解集为________________.
的解集为________________.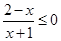 的解集是 .
的解集是 .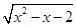 ≥0的解集为________.
≥0的解集为________.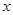 的不等式
的不等式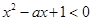 的解集是空集”是假命题,则实数
的解集是空集”是假命题,则实数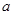 的取值范围是_______.
的取值范围是_______.