题目内容
(1)已知正数a、b满足a+b=1.求:
+
的最小值.
(2)若正实数x、y满足x+y+3=xy,求xy的最小值.
| 1 |
| a |
| 2 |
| b |
(2)若正实数x、y满足x+y+3=xy,求xy的最小值.
(1)∵正数a+b=1,∴
+
=(a+b)(
+
)=3+
+
≥3+2
=3+2
即为最小值,当且仅当a+b=1,
=
,即a=
-1,b=2-
时取等号;
(2)∵正实数x、y满足x+y+3=xy,∴xy≥3+2
,化为(
-3)(
+1)≥0,∴
≥3,即xy≥9,当且仅当x=y=3时取等号,∴xy的最小值为9.
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
| b |
| a |
| 2a |
| b |
| 2 |
| 2 |
(2)∵正实数x、y满足x+y+3=xy,∴xy≥3+2
| xy |
| xy |
| xy |
| xy |

练习册系列答案
相关题目

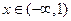 ,则函数
,则函数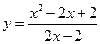 有( )
有( )

