题目内容
函数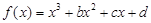 在区间
在区间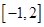 上是减函数,则
上是减函数,则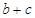 的最大值为 .
的最大值为 .
【答案】
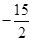
【解析】
试题分析:这类问题首先是通过导数研究函数的单调性,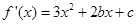 ,
,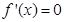 显然有两不等实根
显然有两不等实根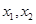 ,从题意上看
,从题意上看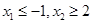 ,即
,即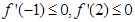 ,∴
,∴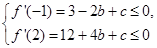 ,由此求
,由此求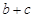 的最大值,可归结为线性规划问题,也可用不等式知识解决,两式直接相加,即
的最大值,可归结为线性规划问题,也可用不等式知识解决,两式直接相加,即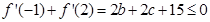 ,
,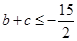 (
(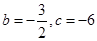 时等号成立).
时等号成立).
考点:函数的单调性.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 在区间
在区间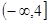 上是减函数,则实数
上是减函数,则实数 的取值范围是_____________
的取值范围是_____________ 在区间
在区间 上是减函数,在区间
上是减函数,在区间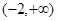 上是增函数,则
上是增函数,则 _______.
_______.  在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围为
。
的取值范围为
。 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围是
的取值范围是 B .
B . C .
C . D
.
D
.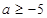
 在区间
在区间 上是减函数,那么
上是减函数,那么 有( )
有( )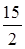 B.最大值
B.最大值 C.最小值
C.最小值