ЬтФПФкШн
вбжЊAЁЂDЗжБ№ЮЊЭждВEЃК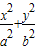 =1ЃЈaЃОbЃО0ЃЉЕФзѓЖЅЕугыЩЯЖЅЕуЃЌЭждВЕФРыаФТЪe=
=1ЃЈaЃОbЃО0ЃЉЕФзѓЖЅЕугыЩЯЖЅЕуЃЌЭждВЕФРыаФТЪe=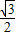 ЃЌF1ЁЂF2ЮЊЭждВЕФзѓЁЂгвНЙЕуЃЌЕуPЪЧЯпЖЮADЩЯЕФШЮвЛЕуЃЌЧв
ЃЌF1ЁЂF2ЮЊЭждВЕФзѓЁЂгвНЙЕуЃЌЕуPЪЧЯпЖЮADЩЯЕФШЮвЛЕуЃЌЧв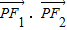 ЕФзюДѓжЕЮЊ1ЃЎ
ЕФзюДѓжЕЮЊ1ЃЎЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЎ
ЃЈ2ЃЉЪЧЗёДцдкдВаФдкдЕуЕФдВЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЌЧвOAЁЭOBЃЈOЮЊзјБъдЕуЃЉЃЌШєДцдкЃЌЧѓГіИУдВЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЩшжБЯпlгыдВCЃКx2+y2=R2ЃЈ1ЃМRЃМ2ЃЉЯрЧагкA1ЃЌЧвlгыЭждВEгаЧвНігавЛИіЙЋЙВЕуB1ЃЌЕБRЮЊКЮжЕЪБЃЌ|A1B1|ШЁзюДѓжЕЃПВЂЧѓзюДѓжЕЃЎ
ЁОД№АИЁПЗжЮіЃКЃЈ1ЃЉЩшPЃЈxЃЌyЃЉЃЌF1ЃЈ-cЃЌ0ЃЉЃЌF2ЃЈcЃЌ0ЃЉЃЌдђ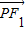
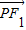 •
•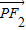 =x2+y2-c2ЃЌPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌЫљвдPдкAЕуЃЌx2+y2зюДѓЃЌa2-c2=1ЃЌгЩДЫФмЧѓГіЭждВЗНГЬ1ЃЎ
=x2+y2-c2ЃЌPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌЫљвдPдкAЕуЃЌx2+y2зюДѓЃЌa2-c2=1ЃЌгЩДЫФмЧѓГіЭждВЗНГЬ1ЃЎ
ЃЈ2ЃЉгЩЭждВЗНГЬЮЊ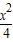 +y2=1ЃЌЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎНтЗНГЬзщ
+y2=1ЃЌЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎНтЗНГЬзщ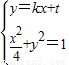 ЕУЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌвЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0ЃЎгЩДЫФмЧѓГіДцдкдВаФдкдЕуЕФдВx2+y2=
ЕУЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌвЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0ЃЎгЩДЫФмЧѓГіДцдкдВаФдкдЕуЕФдВx2+y2= ЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЈ3ЃЉЩшжБЯпlЕФЗНГЬЮЊy=mx+nЃЌвђЮЊжБЯпlгыдВCЃКx2+y2=R2ЃЈ1ЃМRЃМ2ЃЉЯрЧагкA1ЃЌгЩR=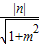 ЃЌжЊn2=R2ЃЈ1+m2ЃЉЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌЫљвд
ЃЌжЊn2=R2ЃЈ1+m2ЃЉЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌЫљвд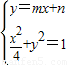 ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЎгЩДЫШыЪжФмЙЛЕМГіЕБR=
ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЎгЩДЫШыЪжФмЙЛЕМГіЕБR=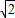 ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉЩшPЃЈxЃЌyЃЉЃЌF1ЃЈ-cЃЌ0ЃЉЃЌF2ЃЈcЃЌ0ЃЉЃЌЦфжаc2=a2-b2ЃЌcЃО0
дђ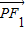 =ЃЈ-c-xЃЌ-yЃЉЃЌ
=ЃЈ-c-xЃЌ-yЃЉЃЌ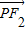 =ЃЈc-xЃЌ-yЃЉЁр
=ЃЈc-xЃЌ-yЃЉЁр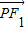 •
•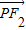 =x2+y2-c2
=x2+y2-c2
ЁпPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌ
ЁрPдкAЕуЃЌx2+y2зюДѓЃЌЁрa2-c2=1ЃЌ
гжe=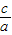 =
=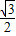 ЃЌЁрa2=4ЃЌb2=1ЃЌc2=3ЃЌЭждВЗНГЬ
ЃЌЁрa2=4ЃЌb2=1ЃЌc2=3ЃЌЭждВЗНГЬ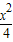 +y2=1ЃЎ
+y2=1ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЭждВЗНГЬЮЊ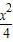 +y2=1ЃЌ
+y2=1ЃЌ
ЂйЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎ
НтЗНГЬзщ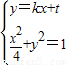 ЕУx2+4ЃЈkx+tЃЉ2=4ЃЌМДЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌ
ЕУx2+4ЃЈkx+tЃЉ2=4ЃЌМДЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌ
вЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0
МД4k2-t2+1ЃО0ЃЌМДt2ЃМ4k2+1ЃЌЧв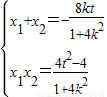 ЃЌ
ЃЌ
y1y2=ЃЈkx1+tЃЉЃЈkx2+tЃЉ=k2x1x2+ktЃЈx1+x2ЃЉ+t2=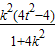 -
-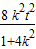 +t2=
+t2=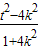 ЃЌ
ЃЌ
вЊЪЙ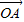 ЁЭ
ЁЭ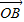 ЃЌашЪЙx1x2+y1y2=0ЃЌМД
ЃЌашЪЙx1x2+y1y2=0ЃЌМД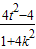 +
+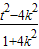 =
=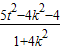 =0ЃЌ
=0ЃЌ
Ыљвд5t2-4k2-4=0ЃЌМД5t2=4k2+4Чвt2ЃМ4k2+1ЃЌМД4k2+4ЃМ20k2+5КуГЩСЂЃЎ
гжвђЮЊжБЯпy=kx+tЮЊдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЃЌ
ЫљвддВЕФАыОЖЮЊr=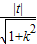 ЃЌr2=
ЃЌr2=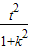 =
=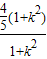 =
= ЃЌЫљЧѓЕФдВЮЊx2+y2=
ЃЌЫљЧѓЕФдВЮЊx2+y2= ЃЎ
ЃЎ
ЂкЕБЧаЯпЕФаБТЪВЛДцдкЪБЃЌЧаЯпЮЊx=±
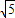 ЃЌгы
ЃЌгы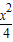 +y2=1НЛгкЕуЃЈ
+y2=1НЛгкЕуЃЈ
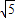 ЃЌ±
ЃЌ±
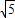 ЃЉЛђЃЈ-
ЃЉЛђЃЈ-
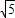 ЃЌ±
ЃЌ±
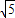 ЃЉТњзуЃЎ
ЃЉТњзуЃЎ
злЩЯЃЌДцдкдВаФдкдЕуЕФдВx2+y2= ЃЎЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЎЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЈ3ЃЉЩшжБЯпlЕФЗНГЬЮЊy=mx+nЃЌвђЮЊжБЯпlгыдВCЃКx2+y2=R2ЃЈ1ЃМRЃМ2ЃЉЯрЧагкA1ЃЌ
гЩЃЈ2ЃЉжЊR=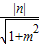 ЃЌМДn2=R2ЃЈ1+m2ЃЉЂйЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌ
ЃЌМДn2=R2ЃЈ1+m2ЃЉЂйЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌ
гЩЃЈ2ЃЉжЊ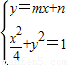 ЕУx2+4ЃЈmx+nЃЉ2=4ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЌ
ЕУx2+4ЃЈmx+nЃЉ2=4ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЌ
дђЁї=64m2n2-16ЃЈ1+4m2ЃЉЃЈn2-1ЃЉ=16ЃЈ4m2-n2+1ЃЉ=0ЃЌМД4m2-n2+1=0ЃЌЂк
гЩЂйЂкЕУ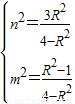 ДЫЪБAЃЌBжиКЯЮЊB1ЃЈx1ЃЌy1ЃЉЕуЃЌгЩ
ДЫЪБAЃЌBжиКЯЮЊB1ЃЈx1ЃЌy1ЃЉЕуЃЌгЩ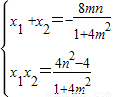 жаx1=x2ЃЌЫљвдx12=
жаx1=x2ЃЌЫљвдx12=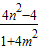 =
=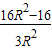 ЃЌB1ЃЈx1ЃЌy1ЃЉЕудкЭждВЩЯЃЌЫљвдy12=1-
ЃЌB1ЃЈx1ЃЌy1ЃЉЕудкЭждВЩЯЃЌЫљвдy12=1- x12=
x12=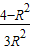
|OB1|2=x12+y12=5-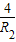 ЃЌдкжБНЧШ§НЧаЮOA1B1жаЃЌ|A1B1|2=|OB1|2-|OA1|2=5-
ЃЌдкжБНЧШ§НЧаЮOA1B1жаЃЌ|A1B1|2=|OB1|2-|OA1|2=5-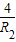 -R2=5-ЃЈ
-R2=5-ЃЈ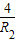 +R2ЃЉ
+R2ЃЉ
вђЮЊЃЈ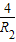 +R2ЃЉЁн4ЕБЧвНіЕБR=
+R2ЃЉЁн4ЕБЧвНіЕБR=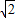 ЁЪЃЈ1ЃЌ2ЃЉЪБШЁЕШКХЃЌЫљвд|A1B1|2Ём5-4=1
ЁЪЃЈ1ЃЌ2ЃЉЪБШЁЕШКХЃЌЫљвд|A1B1|2Ём5-4=1
МДЕБR=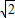 ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
ЕуЦРЃКБОЬтжївЊПМВщжБЯпгыдВзЖЧњЯпЕФзлКЯгІгУФмСІЃЌОпЬхЩцМАЕНЙьМЃЗНГЬЕФЧѓЗЈМАжБЯпгыЭждВЕФЯрЙижЊЪЖЃЌНтЬтЪБвЊШЯецЩѓЬтЃЌзЂвтЭкОђЬтЩшжаЕФвўЬѕМўЃЌСщЛюдЫгУЭждВаджЪЃЌКЯРэЕиНјааЕШМлзЊЛЏЃЎ
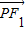
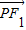 •
•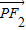 =x2+y2-c2ЃЌPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌЫљвдPдкAЕуЃЌx2+y2зюДѓЃЌa2-c2=1ЃЌгЩДЫФмЧѓГіЭждВЗНГЬ1ЃЎ
=x2+y2-c2ЃЌPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌЫљвдPдкAЕуЃЌx2+y2зюДѓЃЌa2-c2=1ЃЌгЩДЫФмЧѓГіЭждВЗНГЬ1ЃЎЃЈ2ЃЉгЩЭждВЗНГЬЮЊ
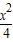 +y2=1ЃЌЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎНтЗНГЬзщ
+y2=1ЃЌЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎНтЗНГЬзщ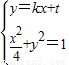 ЕУЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌвЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0ЃЎгЩДЫФмЧѓГіДцдкдВаФдкдЕуЕФдВx2+y2=
ЕУЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌвЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0ЃЎгЩДЫФмЧѓГіДцдкдВаФдкдЕуЕФдВx2+y2= ЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎЃЈ3ЃЉЩшжБЯпlЕФЗНГЬЮЊy=mx+nЃЌвђЮЊжБЯпlгыдВCЃКx2+y2=R2ЃЈ1ЃМRЃМ2ЃЉЯрЧагкA1ЃЌгЩR=
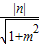 ЃЌжЊn2=R2ЃЈ1+m2ЃЉЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌЫљвд
ЃЌжЊn2=R2ЃЈ1+m2ЃЉЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌЫљвд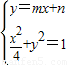 ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЎгЩДЫШыЪжФмЙЛЕМГіЕБR=
ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЎгЩДЫШыЪжФмЙЛЕМГіЕБR=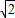 ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎНтД№ЃКНтЃКЃЈ1ЃЉЩшPЃЈxЃЌyЃЉЃЌF1ЃЈ-cЃЌ0ЃЉЃЌF2ЃЈcЃЌ0ЃЉЃЌЦфжаc2=a2-b2ЃЌcЃО0
дђ
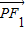 =ЃЈ-c-xЃЌ-yЃЉЃЌ
=ЃЈ-c-xЃЌ-yЃЉЃЌ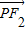 =ЃЈc-xЃЌ-yЃЉЁр
=ЃЈc-xЃЌ-yЃЉЁр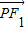 •
•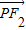 =x2+y2-c2
=x2+y2-c2ЁпPдкADЩЯЃЌx2+y2ПДзїЯпЖЮADЩЯЕФЕуPЃЈxЃЌyЃЉЕНдЕуОрРыЕФЦНЗНЃЌ
ЁрPдкAЕуЃЌx2+y2зюДѓЃЌЁрa2-c2=1ЃЌ
гжe=
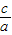 =
=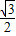 ЃЌЁрa2=4ЃЌb2=1ЃЌc2=3ЃЌЭждВЗНГЬ
ЃЌЁрa2=4ЃЌb2=1ЃЌc2=3ЃЌЭждВЗНГЬ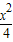 +y2=1ЃЎ
+y2=1ЃЎЃЈ2ЃЉгЩЃЈ1ЃЉжЊЭждВЗНГЬЮЊ
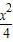 +y2=1ЃЌ
+y2=1ЃЌЂйЩшдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЮЊy=kx+tЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎ
НтЗНГЬзщ
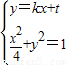 ЕУx2+4ЃЈkx+tЃЉ2=4ЃЌМДЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌ
ЕУx2+4ЃЈkx+tЃЉ2=4ЃЌМДЃЈ1+4kЃЉ2x2+8ktx+4t2-4=0ЃЌвЊЪЙЧаЯпгыЭждВКугаСНИіНЛЕуAЃЌBЃЌдђЪЙЁї=64k2t2-16ЃЈ1+4k2ЃЉЃЈt2-1ЃЉ=16ЃЈ4k2-t2+1ЃЉЃО0
МД4k2-t2+1ЃО0ЃЌМДt2ЃМ4k2+1ЃЌЧв
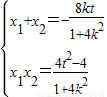 ЃЌ
ЃЌy1y2=ЃЈkx1+tЃЉЃЈkx2+tЃЉ=k2x1x2+ktЃЈx1+x2ЃЉ+t2=
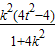 -
-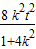 +t2=
+t2=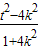 ЃЌ
ЃЌвЊЪЙ
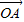 ЁЭ
ЁЭ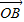 ЃЌашЪЙx1x2+y1y2=0ЃЌМД
ЃЌашЪЙx1x2+y1y2=0ЃЌМД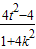 +
+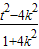 =
=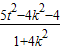 =0ЃЌ
=0ЃЌЫљвд5t2-4k2-4=0ЃЌМД5t2=4k2+4Чвt2ЃМ4k2+1ЃЌМД4k2+4ЃМ20k2+5КуГЩСЂЃЎ
гжвђЮЊжБЯпy=kx+tЮЊдВаФдкдЕуЕФдВЕФвЛЬѕЧаЯпЃЌ
ЫљвддВЕФАыОЖЮЊr=
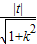 ЃЌr2=
ЃЌr2=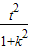 =
=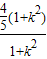 =
= ЃЌЫљЧѓЕФдВЮЊx2+y2=
ЃЌЫљЧѓЕФдВЮЊx2+y2= ЃЎ
ЃЎЂкЕБЧаЯпЕФаБТЪВЛДцдкЪБЃЌЧаЯпЮЊx=±

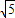 ЃЌгы
ЃЌгы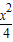 +y2=1НЛгкЕуЃЈ
+y2=1НЛгкЕуЃЈ
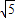 ЃЌ±
ЃЌ±
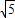 ЃЉЛђЃЈ-
ЃЉЛђЃЈ-
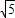 ЃЌ±
ЃЌ±
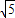 ЃЉТњзуЃЎ
ЃЉТњзуЃЎзлЩЯЃЌДцдкдВаФдкдЕуЕФдВx2+y2=
 ЃЎЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎ
ЃЎЃЌЪЙЕУИУдВЕФШЮвтвЛЬѕЧаЯпгыЭждВEКугаСНИіНЛЕуAЃЌBЃЎЃЈ3ЃЉЩшжБЯпlЕФЗНГЬЮЊy=mx+nЃЌвђЮЊжБЯпlгыдВCЃКx2+y2=R2ЃЈ1ЃМRЃМ2ЃЉЯрЧагкA1ЃЌ
гЩЃЈ2ЃЉжЊR=
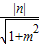 ЃЌМДn2=R2ЃЈ1+m2ЃЉЂйЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌ
ЃЌМДn2=R2ЃЈ1+m2ЃЉЂйЃЌвђЮЊlгыЭждВжЛгавЛИіЙЋЙВЕуB1ЃЌгЩЃЈ2ЃЉжЊ
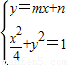 ЕУx2+4ЃЈmx+nЃЉ2=4ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЌ
ЕУx2+4ЃЈmx+nЃЉ2=4ЃЌМДЃЈ1+4m2ЃЉx2+8mx+4n2-4=0гаЮЈвЛНтЃЌдђЁї=64m2n2-16ЃЈ1+4m2ЃЉЃЈn2-1ЃЉ=16ЃЈ4m2-n2+1ЃЉ=0ЃЌМД4m2-n2+1=0ЃЌЂк
гЩЂйЂкЕУ
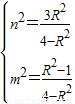 ДЫЪБAЃЌBжиКЯЮЊB1ЃЈx1ЃЌy1ЃЉЕуЃЌгЩ
ДЫЪБAЃЌBжиКЯЮЊB1ЃЈx1ЃЌy1ЃЉЕуЃЌгЩ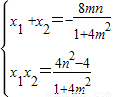 жаx1=x2ЃЌЫљвдx12=
жаx1=x2ЃЌЫљвдx12=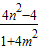 =
=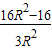 ЃЌB1ЃЈx1ЃЌy1ЃЉЕудкЭждВЩЯЃЌЫљвдy12=1-
ЃЌB1ЃЈx1ЃЌy1ЃЉЕудкЭждВЩЯЃЌЫљвдy12=1- x12=
x12=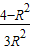
|OB1|2=x12+y12=5-
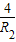 ЃЌдкжБНЧШ§НЧаЮOA1B1жаЃЌ|A1B1|2=|OB1|2-|OA1|2=5-
ЃЌдкжБНЧШ§НЧаЮOA1B1жаЃЌ|A1B1|2=|OB1|2-|OA1|2=5-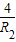 -R2=5-ЃЈ
-R2=5-ЃЈ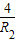 +R2ЃЉ
+R2ЃЉвђЮЊЃЈ
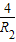 +R2ЃЉЁн4ЕБЧвНіЕБR=
+R2ЃЉЁн4ЕБЧвНіЕБR=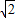 ЁЪЃЈ1ЃЌ2ЃЉЪБШЁЕШКХЃЌЫљвд|A1B1|2Ём5-4=1
ЁЪЃЈ1ЃЌ2ЃЉЪБШЁЕШКХЃЌЫљвд|A1B1|2Ём5-4=1МДЕБR=
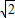 ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎ
ЁЪЃЈ1ЃЌ2ЃЉЪБ|A1B1|ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ1ЃЎЕуЦРЃКБОЬтжївЊПМВщжБЯпгыдВзЖЧњЯпЕФзлКЯгІгУФмСІЃЌОпЬхЩцМАЕНЙьМЃЗНГЬЕФЧѓЗЈМАжБЯпгыЭждВЕФЯрЙижЊЪЖЃЌНтЬтЪБвЊШЯецЩѓЬтЃЌзЂвтЭкОђЬтЩшжаЕФвўЬѕМўЃЌСщЛюдЫгУЭждВаджЪЃЌКЯРэЕиНјааЕШМлзЊЛЏЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
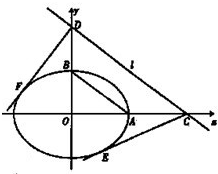 ШчЭМЃЌвбжЊAЃЌBЗжБ№ЮЊЭждВ
ШчЭМЃЌвбжЊAЃЌBЗжБ№ЮЊЭждВ| x2 |
| a2 |
| y2 |
| b2 |
AЁЂЁР
| ||
BЁЂЁР
| ||
CЁЂЁР
| ||
DЁЂЁР
|
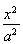
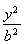
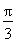
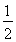
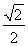

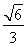
 ЕФзѓЖЅЕугыЩЯЖЅЕуЃЌЭждВЕФРыаФТЪ
ЕФзѓЖЅЕугыЩЯЖЅЕуЃЌЭждВЕФРыаФТЪ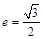 ЃЌF1ЁЂF2ЮЊЭждВЕФзѓЁЂгвНЙЕуЃЌЕуPЪЧЯпЖЮADЩЯЕФШЮвЛЕуЃЌЧв
ЃЌF1ЁЂF2ЮЊЭждВЕФзѓЁЂгвНЙЕуЃЌЕуPЪЧЯпЖЮADЩЯЕФШЮвЛЕуЃЌЧв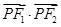 ЕФзюДѓжЕЮЊ1 ЃЎ
ЕФзюДѓжЕЮЊ1 ЃЎ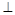 OBЃЈOЮЊзјБъдЕуЃЉЃЌШєДцдкЃЌЧѓГіИУдВЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
OBЃЈOЮЊзјБъдЕуЃЉЃЌШєДцдкЃЌЧѓГіИУдВЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ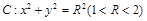 ЯрЧагкA1ЃЌЧвlгыЭждВEгаЧвНігавЛИіЙЋЙВЕуB1ЃЌЕБRЮЊКЮжЕЪБЃЌ|A1B1|ШЁЕУзюДѓжЕЃПВЂЧѓзюДѓжЕЃЎ
ЯрЧагкA1ЃЌЧвlгыЭждВEгаЧвНігавЛИіЙЋЙВЕуB1ЃЌЕБRЮЊКЮжЕЪБЃЌ|A1B1|ШЁЕУзюДѓжЕЃПВЂЧѓзюДѓжЕЃЎ