题目内容
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′,连接EF,A′B.

(1)求证:A′D⊥EF;
(2)求二面角A′-EF-D的余弦值.

(1)求证:A′D⊥EF;
(2)求二面角A′-EF-D的余弦值.
分析:(1)根据平面图形折叠后的不变量可得A'D⊥A'E,A'D⊥A'F,然后利用线面垂直的判定得到线面垂直,从而得到线线垂直;
(2)由题意可得BE=BF,DE=DF,连结BD交EF于点G,连接A'G,则可证明∠A'GD为二面角A'-EF-D的平面角,然后利用解直角三角形即可得到答案.
(2)由题意可得BE=BF,DE=DF,连结BD交EF于点G,连接A'G,则可证明∠A'GD为二面角A'-EF-D的平面角,然后利用解直角三角形即可得到答案.
解答: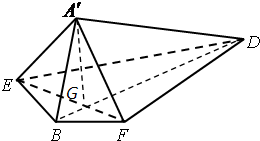 (1)证明:在正方形ABCD中,有AD⊥AE,CD⊥CF
(1)证明:在正方形ABCD中,有AD⊥AE,CD⊥CF
则A'D⊥A'E,A'D⊥A'F
又A'E∩A'F=A'
∴A'D⊥平面A'EF
而EF?平面A'EF,∴A'D⊥EF
(2)方法一:连接BD交EF于点G,连接A'G
∵在正方形ABCD中,点E是AB的中点,点F是BC的中点,
∴BE=BF,DE=DF,
∴点G为EF的中点,
且BD⊥EF
∵正方形ABCD的边长为2,∴A'E=A'F=1,∴A'G⊥EF
∴∠A'GD为二面角A'-EF-D的平面角
由(1)可得A'D⊥A'G,
∴△A'DG为直角三角形
∵正方形ABCD的边长为2,
∴BD=2
,EF=
,
∴BG=
,DG=2
-
=
,
又A'D=2
∴A′G=
=
=
∴cos∠A′GD=
=
=
∴二面角A'-EF-D的余弦值为
方法二:∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,
∴BE=BF=A'E=A'F=1,
∴EF=
∴A'E2+A'F2=EF2,∴A'E⊥A'F
由(1)得A'D⊥平面A'EF,
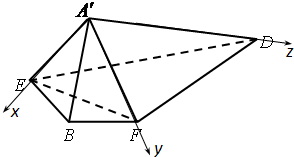
∴分别以A'E,A'F,A'D为x,y,z轴建立如图所示的空间直角
坐标系A'-xyz,
则A'(0,0,0),E(1,0,0),F(0,1,0),D(0,0,2)
∴
=(1,0,-2),
=(0,1,-2),
设平面DEF的一个法向量为
=(x,y,z),则由
,
可取
=(2,2,1)
又平面A'EF的一个法向量可取
=(0,0,1)
∴cos<
,
>=
=
=
∴二面角A'-EF-D的余弦值为
.
 (1)证明:在正方形ABCD中,有AD⊥AE,CD⊥CF
(1)证明:在正方形ABCD中,有AD⊥AE,CD⊥CF则A'D⊥A'E,A'D⊥A'F
又A'E∩A'F=A'
∴A'D⊥平面A'EF
而EF?平面A'EF,∴A'D⊥EF
(2)方法一:连接BD交EF于点G,连接A'G
∵在正方形ABCD中,点E是AB的中点,点F是BC的中点,
∴BE=BF,DE=DF,
∴点G为EF的中点,
且BD⊥EF
∵正方形ABCD的边长为2,∴A'E=A'F=1,∴A'G⊥EF
∴∠A'GD为二面角A'-EF-D的平面角
由(1)可得A'D⊥A'G,
∴△A'DG为直角三角形
∵正方形ABCD的边长为2,
∴BD=2
| 2 |
| 2 |
∴BG=
| ||
| 2 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
又A'D=2
∴A′G=
| DG2-A′D2 |
|
| ||
| 2 |
∴cos∠A′GD=
| A′G |
| DG |
| ||||
|
| 1 |
| 3 |
∴二面角A'-EF-D的余弦值为
| 1 |
| 3 |

方法二:∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,
∴BE=BF=A'E=A'F=1,
∴EF=
| 2 |
∴A'E2+A'F2=EF2,∴A'E⊥A'F
由(1)得A'D⊥平面A'EF,
∴分别以A'E,A'F,A'D为x,y,z轴建立如图所示的空间直角
坐标系A'-xyz,
则A'(0,0,0),E(1,0,0),F(0,1,0),D(0,0,2)
∴
| DE |
| DF |
设平面DEF的一个法向量为
| n1 |
|
可取
| n1 |
又平面A'EF的一个法向量可取
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| 1 | ||
|
| 1 |
| 3 |
∴二面角A'-EF-D的余弦值为
| 1 |
| 3 |
点评:本题考查了直线与平面垂直的性质,考查了二面角的平面角及其求法,利用空间向量求解是新课标意图的体现,关键是建立正确的空间右手系,此题是中档题.

练习册系列答案
相关题目
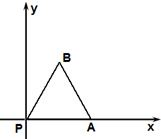 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.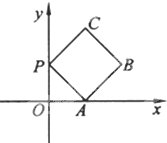 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为