题目内容
函数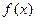 的定义域为R,对任意实数x满足f(x-2)=f(4-x),且f(x-1)=f(x-3),当1≤x≤2时,f(x)=x2,则f(x)的单调区间为(以下k∈Z) ( )
的定义域为R,对任意实数x满足f(x-2)=f(4-x),且f(x-1)=f(x-3),当1≤x≤2时,f(x)=x2,则f(x)的单调区间为(以下k∈Z) ( )
A.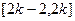 | B.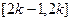 | C.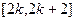 | D.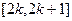 |
D
解析

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若奇函数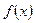 在
在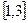 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在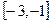 上( )
上( )
| A.是减函数,有最小值0 | B.是增函数,有最小值0 | C.是减函数,有最大值0 | D.是增函数,有最大值0 |
 的反函数为 ( )
的反函数为 ( )
A. | B. |
C. | D. |
已知函数 满足
满足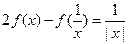 ,则
,则 的最小值是( )
的最小值是( )
| A.2 | B.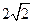 | C.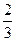 | D.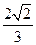 |
图中的图象所表示的函数的解析式为( )
A.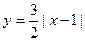 (0≤x≤2) (0≤x≤2) |
B.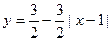 (0≤x≤2) (0≤x≤2) |
C.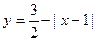 (0≤x≤2) (0≤x≤2) |
D.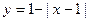 (0≤x≤2) (0≤x≤2) |
函数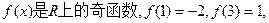 则 ( )
则 ( )
A.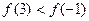 | B. |
C.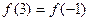 | D.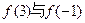 的大小不能确定 的大小不能确定 |
已知函数f (x) = 3-2 |x|, g(x) = x2-2x,构造函数y = F(x),定义如下:当f (x)≥g (x)时,F(x) = g(x);当f ( x) < g (
x) < g ( x)时,F(x) = f (x),那么F(x) ( )
x)时,F(x) = f (x),那么F(x) ( )
| A.有最大值3,最小值-1 | B.有最大值3,无最小值 |
C.有最大值7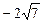 ,无最小值 ,无最小值 | D.无最大值,也无最小值 |
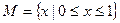 为定义域,以
为定义域,以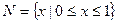 为值域的函数是( )
为值域的函数是( )