题目内容
甲、乙两名篮球队员轮流投篮直至某人投中为止,设甲每次投篮命中的概率为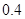 ,乙投中的概率为
,乙投中的概率为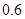 ,而且不受其他次投篮结果的影响,设投篮的轮数为
,而且不受其他次投篮结果的影响,设投篮的轮数为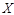 ,若甲先投,则
,若甲先投,则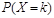 等于( )
等于( )
A.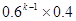 B. 0.24k-1×0.4
C.
B. 0.24k-1×0.4
C. 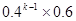 D.
D. 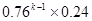
【答案】
B
【解析】
试题分析:∵甲和乙投篮不受其他投篮结果的影响,∴本题是一个相互独立事件同时发生的概率,
∵每次投篮甲投中的概率为0.4,乙投中的概率为0.6,
甲投篮的次数为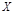 ,甲先投,则
,甲先投,则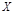 =k表示甲第K次投中篮球,而乙前k-1次没有投中,
=k表示甲第K次投中篮球,而乙前k-1次没有投中,
根据相互独立事件同时发生的概率得到0.4k-1×0.6k-1×0.4=0.24k-1×0.4;故选B.
考点:本题主要考查相互独立事件的概率乘法公式.
点评:是一个基础题,本题最大的障碍是理解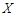 =k的意义,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式。
=k的意义,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目