题目内容
(原创)函数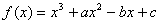 ,
,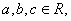 已知方程
已知方程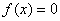 有三个实根
有三个实根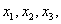 即
即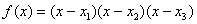
(1)求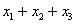 ,
,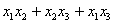 和
和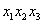 的值.(结果用
的值.(结果用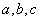 表示)
表示)
(2)若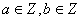 且
且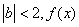 在
在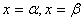 处取得极值且
处取得极值且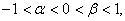 试求此方程三个根两两不等时
试求此方程三个根两两不等时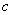 的取值范围.
的取值范围.
【答案】
解:(1)由已知,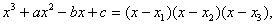 比较两边系数,得
比较两边系数,得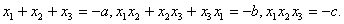
(2)由已知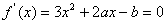 有两个不等的实根
有两个不等的实根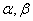 因为
因为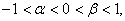 由实根分布,则
由实根分布,则
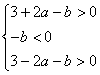
由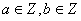 ,
,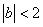 则
则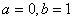 .所以
.所以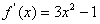
则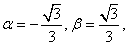
且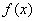 在
在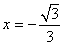 处取得极大值
处取得极大值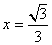 取得极小值,
取得极小值,
故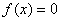 要有三个不等根,则必须
要有三个不等根,则必须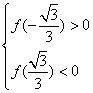
解得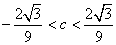 .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
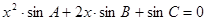 有两等根,则
有两等根,则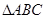 的三边
的三边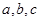 满足关系式( )
满足关系式( )
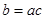 B.
B.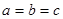 C.
C.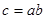 D.
D.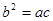
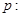 方程
方程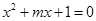 有两个不相等的负实根;
有两个不相等的负实根;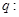 方程
方程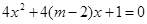 无实根,若"
无实根,若"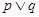 "为真,"
"为真,"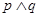 "为假,求
"为假,求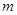 的取值范围。
的取值范围。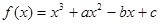 ,
, 已知方程
已知方程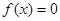 有三个实根
有三个实根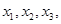 即
即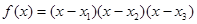
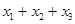 ,
, 和
和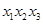 的值.(结果用
的值.(结果用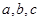 表示)
表示)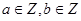 且
且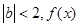 在
在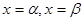 处取得极值且
处取得极值且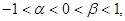 试求此方程三个根两两不等时
试求此方程三个根两两不等时 的取值范围.
的取值范围.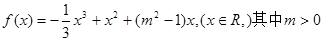 .
.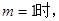 曲线
曲线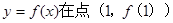 处的切线斜率;
处的切线斜率;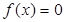 有三个互不相同的实根0,
有三个互不相同的实根0,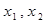 ,且
,且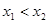 .若对任意的
.若对任意的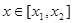 ,
,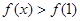 恒成立,求m的取值范围
恒成立,求m的取值范围