Question

已知p：x∈A={x|x²-2x-3≤0，x∈R}，q：x∈B={x|x²-2mx+m²-9≤0，x∈R，m∈R}．
（1）若A∩B=[1，3]，求实数m的值；
（2）若p是q的充分不必要条件，求实数m的取值范围．

Answer 1

分析：（1）先求出集合A，B，利用条件A∩B=[1，3]，即可求实数m的值；
（2）利用p是q的充分不必要条件，建立条件关系，即可求实数m的取值范围．

解答：解：（1）A={x|x²-2x-3≤0，x∈R}={x|-1≤x≤3，x∈R}，
B={x|x²-2mx+m²-9≤0，x∈R，m∈R}={x|m-3≤x≤m+3，x∈R，m∈R}，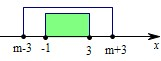
由A∩B=[1，3]，得m-3=1．
即m=4．
（2）∵A={x|-1≤x≤3，x∈R}，B={x|m-3≤x≤m+3，x∈R，m∈R}，
∴要使p是q的充分不必要条件，
则

m-3≤-1 m+3≥3

，
即

m≤2 m≥0

，
∴0≤m≤2

点评：本题主要考查集合的基本运算以及充分条件和必要条件的应用，利用一元二次不等式的解法化简集合M，N是解决本题的关键．