题目内容
（06年广东卷）（12分）
A是由定义在
上且满足如下条件的函数
组成的集合：①对任意
，都有
； ②存在常数
，使得对任意的
，都有
（Ⅰ）设
，证明：
(Ⅱ) 设,如果存在
,使得
,那么这样的
是唯一的;
(Ⅲ) 设,任取
,令
证明:给定正整数k,对任意的正整数p,成立不等式
解析：对任意
,
,
,
,所以
对任意的
，
，
，
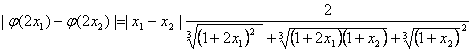所以0<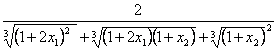
,令=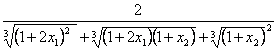
，
，
所以
反证法:设存在两个
使得
,
则
由
，得
，所以
，矛盾，故结论成立。
，所以
+…
练习册系列答案
相关题目
B. 
D. 
的反函数
的图象与y轴交于点
(如图2所示)，则方程
的根是
分别在
、
处取得极小值、极大值.
平面上点A、B的坐标分别为
、
,该平面上动点P满足
,点Q是点P关于直线
的对称点.求：