题目内容
已知函数f(x)= 
,则f[f(2014)]= ( )
| A．1 |
| B．-1 |
| C．0 |
D． |
A
解析∵f(2014)=2014-14=2000
∴f[f(2014)]=f(2000)=cos(
×2000)=cos500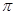
=1
练习册系列答案
阅读快车系列答案
相关题目
下列角中终边与330°相同的角是（ ）
| A．30° | B．-30° | C．630° | D．-630° |
函数
的部分图象如图所示，则
的值分别是
A．2， | B．2， | C．4， | D．4， |
函数
在区间
上可找到
个不同数
，
， ，
，使得
，则的最大值等于（ ）
| A．8 | B．9 | C．10 | D．11 |
将函数
的图象向右平移
个单位，再向下平移1个单位后得到的函数图象对应的表达式为( )
A． | B． |
C． | D． |
已知向量
，下列结论中正确的是（ ）
A． | B． |
C． | D． 、 的夹角为 |
定义某种运算
，运算原理如上图所示，则式子
的值为（ ）
| A．4 | B．8 | C．11 | D．13 |
函数f（x）="sinxcos" x+
cos2x的最小正周期和振幅分别是（ ）
| A．π，1 | B．π，2 | C．2π，1 | D．2π，2 |
已知函数f(x)=sin(2x+
)，其中为实数，若f(x)≤|f(
)|对x∈R恒成立，且f(
)>f(
)，则f(x)的单调递增区间是（ ）
A．[ - ,+](k∈Z) |
| B．[,+](k∈Z) |
C．[+,+ ](k∈Z) |
| D．[-,](k∈Z) |