题目内容
已知函数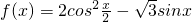 .
.
(Ⅰ)求函数f(x)的最小正周期和值域;
(Ⅱ)若a为第二象限角,且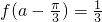 ,求
,求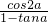 的值.
的值.
解:(Ⅰ)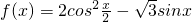 =
=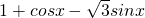 =1+2cos(x+
=1+2cos(x+ )
)
∴函数f(x)的周期为2π,
∵2cos(x+ )∈[-2,2],∴函数的值域为[-1,3]. …(5分)
)∈[-2,2],∴函数的值域为[-1,3]. …(5分)
(Ⅱ)因为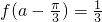 ,所以1+2cosα=
,所以1+2cosα= ,即cosα=-
,即cosα=- . …(6分)
. …(6分)
因为α为第二象限角,所以sinα= .
.
所以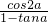 =cosα(cosα+sinα)=-
=cosα(cosα+sinα)=- ×(-
×(- +
+ )=
)=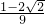 …(13分)
…(13分)
分析:(Ⅰ)利用二倍角公式及辅助角公式化简函数,从而可求函数f(x)的最小正周期和值域;
(Ⅱ)利用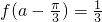 ,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得
,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得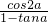 的值.
的值.
点评:本题考查三角函数的化简,考查函数的性质,考查函数值的计算,解题的关键是化简函数.
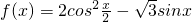 =
=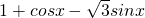 =1+2cos(x+
=1+2cos(x+ )
)∴函数f(x)的周期为2π,
∵2cos(x+
 )∈[-2,2],∴函数的值域为[-1,3]. …(5分)
)∈[-2,2],∴函数的值域为[-1,3]. …(5分)(Ⅱ)因为
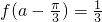 ,所以1+2cosα=
,所以1+2cosα= ,即cosα=-
,即cosα=- . …(6分)
. …(6分)因为α为第二象限角,所以sinα=
 .
. 所以
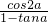 =cosα(cosα+sinα)=-
=cosα(cosα+sinα)=- ×(-
×(- +
+ )=
)=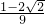 …(13分)
…(13分)分析:(Ⅰ)利用二倍角公式及辅助角公式化简函数,从而可求函数f(x)的最小正周期和值域;
(Ⅱ)利用
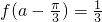 ,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得
,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得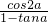 的值.
的值.点评:本题考查三角函数的化简,考查函数的性质,考查函数值的计算,解题的关键是化简函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数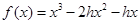 ,若
,若 且
且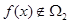 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得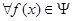 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


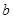
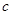




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.