题目内容
以x轴为对称轴，原点为顶点的抛物线上的一点P（1，m）到焦点的距离为3，则其方程是
A.y＝4x2 B. y＝8x2 C. y2＝4x D. y2＝8x
【答案】
D
【解析】
试题分析：根据题意假设抛物线的方程为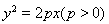
.因为根据抛物线上的一点到焦点的距离等于到准线的距离，即可得
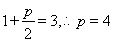.所以抛物线的方程为
.故选D.本小题考查的知识点为抛物线的定义.
考点：1.抛物线的定义.2.数形结合的思想.
练习册系列答案
相关题目
线段AB过x轴正半轴上一定点M（m，0），两端点A、B到x轴的距离之积为2m，O为坐标原点，以x轴为对称轴，经过A、O、B三点作抛物线．
（1）求这条抛物线方程；
（2）若∠AOB=
，求m的最大值．
（1）求这条抛物线方程；
（2）若∠AOB=
| 3π | 4 |
以x轴为对称轴，原点为顶点的抛物线上的一点P（1，m）到焦点的距离为3，则其方程是（ ）
| A、y=4x2 | B、y=8x2 | C、y2=4x | D、y2=8x |