题目内容
不等式log
(x2-x)>x2-x+
的解集为( )
| 1 |
| 2 |
| 1 |
| 2 |
分析:利用换元法设u=x2-x,然后利用对数函数的性质解对数不等式即可,利用数形结合确定不等式的解集.
解答:解:令u=x2-x,不等式log
(x2-x)>x2-x+
?log
u>u+
.
在同一直角坐标系中画函数y1=log
x和y2=x+
的图象,
当x=
时,y1=y2=1,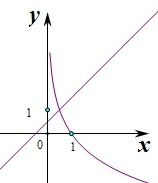
由图象可知满足y1>y2的x的范围为(0,
),
即要求0<u=x2-x<
,解得x∈(
,0)∪(1,
),
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在同一直角坐标系中画函数y1=log
| 1 |
| 2 |
| 1 |
| 2 |
当x=
| 1 |
| 2 |

由图象可知满足y1>y2的x的范围为(0,
| 1 |
| 2 |
即要求0<u=x2-x<
| 1 |
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
故选A.
点评:本题主要考查对数不等式的解法,利用换元法将函数转化为两个基本初等函数,利用数形结合是解决本题的关键.

练习册系列答案
相关题目