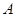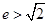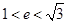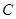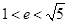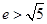题目内容
抛物线2y2+x=0的焦点坐标是 ( )
A.(- ,0) ,0) | B.(0,- ) ) | C.(- ,0) ,0) | D.(0,- ) ) |
C
解析考点:抛物线的简单性质.
专题:计算题.
分析:根据抛物线y2=2px的焦点坐标为F( 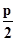 ,0),得到抛物线y2=-
,0),得到抛物线y2=-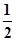 x的2p=-
x的2p=-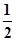 ,
, 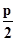 =-
=-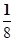 ,所以焦点坐标为(-
,所以焦点坐标为(-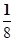 ,0).
,0).
解答:解:∵抛物线的方程是y2=-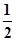 x,
x,
∴2p=-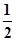 ,得
,得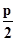 =-
=-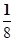 ,
,
∵抛物线y2=2px的焦点坐标为F(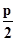 ,0)
,0)
∴抛物线y2=-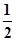 x的焦点坐标为(-
x的焦点坐标为(-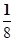 ,0).
,0).
故选C
点评:本题给出抛物线的标准方程,求抛物线的焦点坐标,着重考查了抛物线的标准方程与简单性质,属于基础题.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知双曲线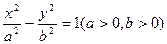 的实轴长、虚轴长、焦距长成等差数列,
的实轴长、虚轴长、焦距长成等差数列,
则此双曲线的离心率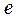 为( )
为( )
| A. | B. | C.2 | D.3 |
双曲线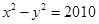 的左、右顶点分别为
的左、右顶点分别为 、
、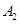 ,P为其右支上的一点,且
,P为其右支上的一点,且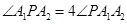 ,则
,则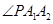 等于( )
等于( )
| A.无法确定 | B.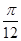 | C.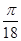 | D.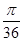 |
若椭圆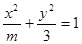 的右焦点与抛物线
的右焦点与抛物线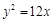 的焦点重合,则
的焦点重合,则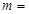
| A.3 | B.6 | C.9 | D.12 |
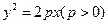 与双曲线
与双曲线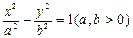 有相同的焦点
有相同的焦点 ,点
,点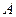 是两曲线的一个交点,且
是两曲线的一个交点,且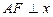 轴,若
轴,若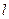 为双曲线的一条斜率大于0的渐近线,则
为双曲线的一条斜率大于0的渐近线,则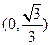
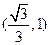
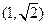

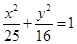 的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )
的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )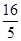
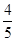
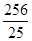
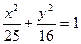 上的一点
上的一点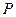 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为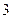 ,则
,则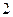 B
B 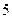 D
D 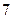
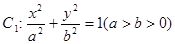 的左准线为
的左准线为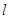 ,左右焦点分别为
,左右焦点分别为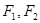 ,抛物线
,抛物线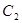 的准线为
的准线为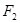 ,曲线
,曲线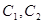 的一个交点为P,则
的一个交点为P,则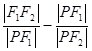 等于()
等于()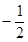 D
D 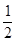
 轴上的双曲线的右焦点,与双曲线的两个交点分别在左、右两只上,则双曲线的离心率的取值范围是 ( )
轴上的双曲线的右焦点,与双曲线的两个交点分别在左、右两只上,则双曲线的离心率的取值范围是 ( )