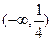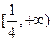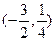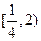题目内容
求函数的定义域和值域．
y＝log2(x2－2x＋2)；
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 5 | 6 | 7 |
y＝log2(x2－2x＋2)；
R．,[0，＋∞).
解：
要使函数有意义，则x2－2x＋2>0，∴x∈R，
函数的定义域为R．
∵x2－2x＋2∈[1，＋∞)，∴函数的值域为[0，＋∞).
要使函数有意义，则x2－2x＋2>0，∴x∈R，
函数的定义域为R．
∵x2－2x＋2∈[1，＋∞)，∴函数的值域为[0，＋∞).
练习册系列答案
相关题目
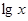；2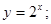
3y = x2; 4y=" |x|" －1;
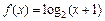，当点(x，y) 是函数y = f (x) 图象上的点时，点
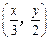是函数y = g(x) 图象上的点．
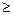0时，求x的取值范围；
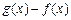的最大值．
（2）
（3）
（4）
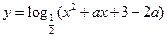在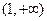
上单调递减，则
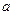的取值范围是
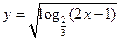的定义域是 （ ）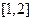
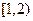
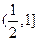
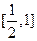
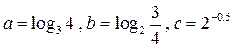，则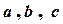
的大小关系（ ）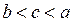
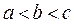
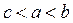
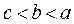
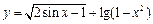的定义域是 ．
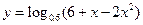的单调递增区间是( )
