题目内容
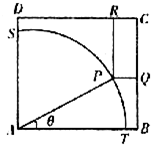 随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.
随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.
(1)设∠PAB=θ,试写出停车场PQCR的面积S与θ的函数关系式;
(2)求长方形停车场PQCR面积的最大值和最小值.
解:(1)延长RP交AB于E,延长QP交AD于F,
由ABCD是正方形,PRCQ是矩形,可知PE⊥AB,PF⊥AD,
∴EP=90cosθ,FP=90sinθ,
∴PR=100-90sinθ,PQ=100-90cosθ,
∴SPQCR=f(θ)=PR•PQ=(100-90cosθ)(100-90sinθ)=8100sinθcosθ-900(sinθ+cosθ)+10000(0°≤θ≤90°);
(2)令sinθ+cosθ=t(1≤t≤ ),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,
),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,
即sinθcosθ=
∴S=10000-9000t+8100× =
= ×
× +950
+950
∴t= 时,Smax=14050-9000
时,Smax=14050-9000 (m2),t=
(m2),t= 时,Smin=950(m2).
时,Smin=950(m2).
分析:(1)延长RP交AB于E,延长QP交AD于F,由ABCD是正方形,推出S关于θ的函数解析式;
(2)设sinθ+cosθ=t,利用平方关系求出sinθcosθ的表达式,通过θ的范围求出t的范围,得到S关于t的表达式,利用二次函数的性质求出S的最大值.
点评:本题考查的重点是函数模型的构建,解题的关键是自变量的选取,利用配方法求函数的最值.

由ABCD是正方形,PRCQ是矩形,可知PE⊥AB,PF⊥AD,
∴EP=90cosθ,FP=90sinθ,
∴PR=100-90sinθ,PQ=100-90cosθ,
∴SPQCR=f(θ)=PR•PQ=(100-90cosθ)(100-90sinθ)=8100sinθcosθ-900(sinθ+cosθ)+10000(0°≤θ≤90°);
(2)令sinθ+cosθ=t(1≤t≤
 ),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,
),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,即sinθcosθ=

∴S=10000-9000t+8100×
 =
= ×
× +950
+950∴t=
 时,Smax=14050-9000
时,Smax=14050-9000 (m2),t=
(m2),t= 时,Smin=950(m2).
时,Smin=950(m2).分析:(1)延长RP交AB于E,延长QP交AD于F,由ABCD是正方形,推出S关于θ的函数解析式;
(2)设sinθ+cosθ=t,利用平方关系求出sinθcosθ的表达式,通过θ的范围求出t的范围,得到S关于t的表达式,利用二次函数的性质求出S的最大值.
点评:本题考查的重点是函数模型的构建,解题的关键是自变量的选取,利用配方法求函数的最值.

练习册系列答案
相关题目
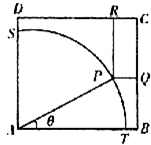 随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.
随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.