题目内容
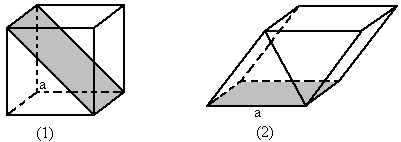
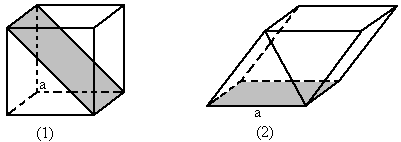
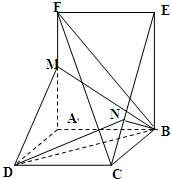 已知如图几何体,正方形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.
已知如图几何体,正方形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.(Ⅰ)求证:CF∥平面BDM;
(Ⅱ)求二面角M-BD-N的大小.
分析:(Ⅰ)证明CF∥平面BDM,利用线面平行的判定,只需证明CF平行于平面BDM中以一条线即可,连接AC,AC∩BD=O,连接OM,则O为AC的中点,根据M为AF的中点,可证OM∥CF;
(Ⅱ)设AB=a,∴BE=2a,求出S△BMD=
a2,S△BND=
a2,可得二面角M-BD-N的平面角的余弦值为
=
=
,由此可求二面角M-BD-N的平面角的大小.
(Ⅱ)设AB=a,∴BE=2a,求出S△BMD=
| ||
| 2 |
| ||
| 5 |
| S△BND |
| S△BMD |
| ||||
|
2
| ||
| 5 |
解答: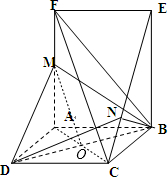 (Ⅰ)证明:连接AC,AC∩BD=O,连接OM,则O为AC的中点
(Ⅰ)证明:连接AC,AC∩BD=O,连接OM,则O为AC的中点
∵M为AF的中点,∴OM∥CF
∵OM?平面BDM,∴CF∥平面BDM;
(Ⅱ)解:设AB=a,∴BE=2a,
在△BEC中,CE=
a,∴BN=
=
a
在△BMD中,DM=BM=DB=
a,∴S△BMD=
a2
∵DC⊥平面BCE,BN?平面BCE,∴DC⊥BN
∵BN⊥CE,DC∩CE=C,∴BN⊥平面DCN,∴BN⊥DN
在△BND中,BN=
a,DN=
a,∴S△BND=
a2
∴二面角M-BD-N的平面角的余弦值为
=
=
∴二面角M-BD-N的平面角的大小为arccos
.
 (Ⅰ)证明:连接AC,AC∩BD=O,连接OM,则O为AC的中点
(Ⅰ)证明:连接AC,AC∩BD=O,连接OM,则O为AC的中点∵M为AF的中点,∴OM∥CF
∵OM?平面BDM,∴CF∥平面BDM;
(Ⅱ)解:设AB=a,∴BE=2a,
在△BEC中,CE=
| 5 |
| BE•BC |
| CE |
| 2 | ||
|
在△BMD中,DM=BM=DB=
| 2 |
| ||
| 2 |
∵DC⊥平面BCE,BN?平面BCE,∴DC⊥BN
∵BN⊥CE,DC∩CE=C,∴BN⊥平面DCN,∴BN⊥DN
在△BND中,BN=
| 2 | ||
|
| ||
|
| ||
| 5 |
∴二面角M-BD-N的平面角的余弦值为
| S△BND |
| S△BMD |
| ||||
|
2
| ||
| 5 |
∴二面角M-BD-N的平面角的大小为arccos
2
| ||
| 5 |
点评:本题考查线面平行,考查面面角,解题的关键是掌握线面平行的判定方法,利用面积射影法求面面角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目